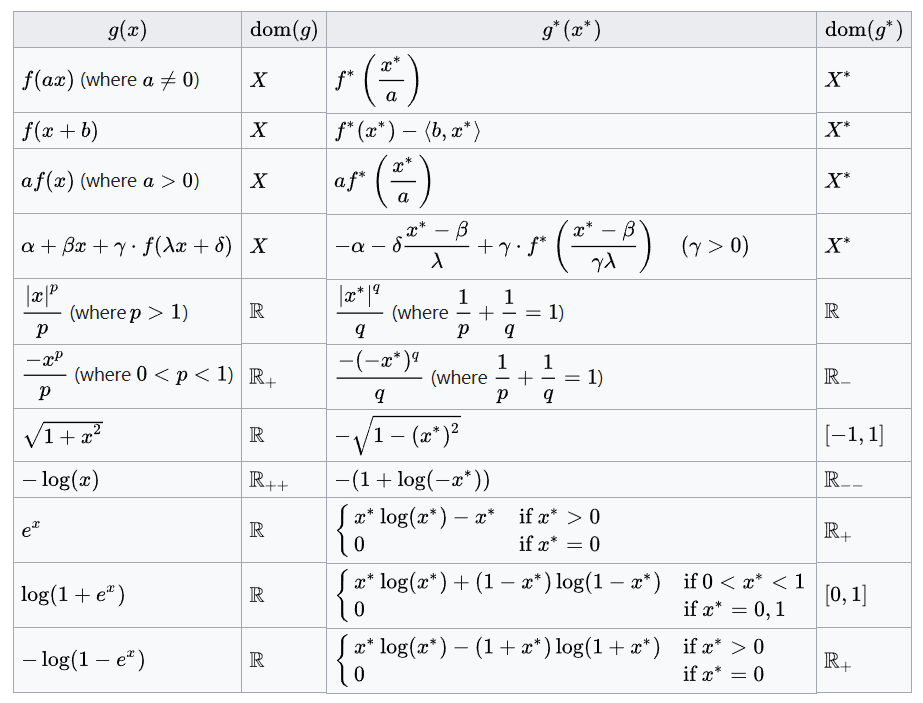前言:主要参考了凸优化理论一书及讨论班上的ppt, $\mathbb{R}$表示实数域.

基本概念

凸集与凸函数

凸集

凸集:

$\mathbb{R}^{n}$的子集$C$被称为凸集,如果其满足$\alpha x+(1-\alpha)y\in C,\forall x,y\in C,\forall \alpha \in [0,1]$.

锥体(cone):

$0\in C$,如果对 $\forall x \in C , \forall \lambda > 0, \lambda x \in C$ ,则称$C$为锥体.

保持集合凸性的运算

凸集在以下几种运算下能保持凸性:

任意多个凸集的交集是凸集.
任意两个凸集的向量和是凸集.
对任意的凸集$C$和标量$\lambda$,集合$\lambda C$是凸集.
凸集的闭包(closure)和内点集(interior)是凸集.
凸集在仿射函数下的像和原像是凸集.

几个特殊的凸集

下面是最常见的几个凸集的例子:

超平面(hyperplane)形如$\{x|a'x=b\}$,其中$a$为非零向量而$b$为标量.
半空间(half space)形如$\{x|a'x\le b\}$,其中$a$为非零向量而$b$为标量.
多面体是有限个半空间的非空交集,形如$\{x|a'_{j}x≤b_{j},j=1,...,r\}$,其中$a_{1},...,a_{r}$和$b_{1},...,b_{r}$分别为$\mathbb{R}^{n}$中的一组向量和标量.
多面体锥(polyhedral cone)形如$\{x|a'_{j}x≤0,j=1,...,r\}$,其中$a_{1},...,a_{r}$为$\mathbb{R}^{n}$中的一组向量.

凸函数

实值凸函数

凸函数：

$C$为$\mathbb{R}^{n}$的凸子集,称函数$f:C\mapsto \mathbb{R}$为凸函数如果\[f(\alpha x+(1-\alpha)x)\le \alpha f(x)+(1-\alpha)f(y),\forall x,y\in C,\forall \alpha \in[0,1]\]

两个凸函数的典型例子是:

仿射函数(affine function),这类函数形如$f(x)=a'x+b$,其中$a\in \mathbb{R}^{n}$而$b\in \mathbb{R}$.
一般的范数函数$║║$,因其满足三角不等式,故均为凸函数.

便捷起见,一般假设函数在定义域上处处取有限值域,但很多优化问题的实际情况中,目标函数尝尝取到无穷大,例如 $f(x)=\sup \limits _ {i\in I} f_{i}(x)$;此外,还有一些函数仅仅定义在某凸子集上,例如$f:(0,+\infty)\mapsto R$,无法把定义域拓展到整个$\mathbb{R}$上,这时最方便的做法就是拓展的部分直接取无穷大.

扩充实值函数

基于上述原因,下面引入扩充实值函数的概念,首先引入几个定义:

上图

考虑定义域为$R^{n}$中的子集$X$的函数$f:X\mapsto [-\infty,+\infty]$,其上图是$\mathbb{R}^{n+1}$的子集,其定义如下:

$epi(f)=\{(x,\omega)|x\in X,\omega\in \mathbb{R},f(x)\le \omega\}$.

这里引用维基上关于上图的定义的一张图简单说明$epi(f)$, 绿色部分就是$epi(f)$.

有效定义域

有效定义域(effective domain):

$dom(f)=\{x\in X|f(x)<\infty\}=\{x|\exists \omega\in \mathbb{R},s.t.(x,\omega)\in epi(f)\}$

扩充实值凸函数

扩充实值凸函数:

令$C$为$\mathbb{R}^{n}$的凸子集,则扩充的实值函数$f:C\mapsto [-\infty,+\infty]$称为凸函数当$epi(f)$是$\mathbb{R}^{n+1}$的凸子集.

仔细比较与上文凸函数的定义不难发现:

$f$的值域由$\mathbb{R}$变成了$[-\infty,+\infty]$.
条件$f(\alpha x+(1-\alpha)y)≤\alpha f(x)+(1-\alpha)f(y),\forall x,y\in C,\forall\alpha\in[0,1]$变成了当$epi(f)$是$\mathbb{R}^{n+1}$的凸子集.

不难看出,若是按照上文的方法定义扩充实值凸函数,容易碰到$\alpha f(x)+(1-\alpha)f(y)$为$\infty$的情况.

** 至此,扩充实值函数的凸性与其上图的凸性的等价关系已经建立. **

在C上的凸函数

出于严谨性,最后补充一种情况,有时还会遇到定义域$C$非凸的函数,且若限制定义域为$C$的凸子集,限制后的函数为凸函数,下面对这种情况的函数$f$给出定义:

在$C$上的凸函数:

$C,X$为$R^{n}$的子集其中$C\subset X$,则称扩充的实值函数$f:X\mapsto [-\infty,+\infty]$称为在$C$上的凸函数,若$f|_{C}$为凸函数.

把定义域$X$替换成$C$,原函数也就是凸函数了,因此这类函数可直接视为凸函数,对其直接用实凸函数的结论.

函数的闭性与半连续性

闭性

闭函数:

如果某个函数$f:X\mapsto [-\infty,+\infty]$的上图是闭集,称$f$为闭函数.

至此,扩充实值函数的闭性与其上图的闭性的等价关系已经建立.

下半连续性

下半连续(lower semicontinuous):

函数$f$是在向量$x\in X$处是下半连续的,如果$f(x)\le \liminf\limits _ {k\to +\infty}f(x_{k})$对每个满足$x_{k}\to x$的点列$\{x_{k}\}\subset X$成立.

闭性与下半连续性的等价

下述定理把函数的下半连续性与闭性等价起来:

对于函数$f:\mathbb{R}^{n}\mapsto [-\infty,+\infty]$,下列陈述等价:

水平集$V_{\gamma}=\{x|f(x)\le\gamma\}$对$\forall\gamma\in R$闭.

$f$下半连续.

$f$闭.

凸函数的运算

类似于在凸集一节中提到的保持集合凸性的运算,保持函数凸性的运算主要有以下几种:

线性变换.
与非负标量相乘.
取上确界.
对部分变量最小化.

可微凸函数

一阶可微凸函数

下面这个命题想必大家都不会陌生:

$C$为$\mathbb{R}^{n}$中的非空闭凸子集,且$f:\mathbb{R}^{n}\mapsto \mathbb{R}$在包含$C$的开集上可微,那么函数$f$在$C$上凸当且仅当\[f(z)\ge f(x)+∇f(x)'(z-x),\forall x,z\in C\]

一张图秒懂上述命题: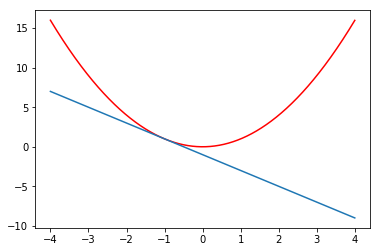

上述命题能导出一个最优性条件:

$C$为$\mathbb{R}^{n}$中的非空闭凸子集,且$f:\mathbb{R}^{n}\mapsto \mathbb{R}$在包含$C$的开集上可微,则向量$x_{0}$在$C$上取最小当且仅当 $∇f(x_{0})'(z-x_{0})\ge 0,\forall z\in C$.

简单证明:

充分性可有Fermat引理得到;
必要性则可由¥$f(z)\ge f(x_{0})+∇f(x)'(z-x_{0})\ge f(x_{0}),\forall z\in C$.

而上述最优性条件又能来证明如下投影定理(Projection Theorem):

$C$为$\mathbb{R}^{n}$中的非空闭凸子集,$z$为$\mathbb{R}^{n}$中的一个向量,则在$x\in C$上存在唯一的向量,使得$║z-x║$最小,这个向量称为$z$在$C$上的投影,记为$x_{0}$.$x_{0}$为$z$在$C$上的投影当且仅当\[(z-x_{0})'(x-x_{0})\le 0,\forall x\in C\]

简单证明:

$x_{0}$为$z$在$C$上的投影等价于$x_{0}$为$║z-x║$最小值点;
又等价于$x_{0}$为$f(x)=1/2║z-x║^{2}$的最小值点;
再将$f(x)$带入上述最优性条件可知$x_{0}$使$f$在$C$上取最小当且仅当$(x_{0}-z)'(x-x_{0})\ge 0,\forall x\in C$.

二阶可微凸函数

下面这个命题想必大家也不会陌生:

$C$为$\mathbb{R}^{n}$中的非空闭凸子集,且$f:\mathbb{R}^{n}\mapsto \mathbb{R}$在包含$C$的开集上二阶可微.

如果$∇^{2}f(x)$对所有的$x\in C$半正定,那么函数$f$在$C$上为凸.

如果$∇^{2}f(x)$对所有的$x\in C$正定,那么函数$f$在$C$上为严格凸.

如果$C$为开,且函数$f$在$C$上凸,那么$∇^{2}f(x)$对所有的$x\in C$半正定.

凸包、仿射包及Carathéodory定理

凸包

凸包(convex hull):

集合$X$的凸包,指所有包含$X$的凸集的交集,记作$conv(X)$.

$X$由图中的小黑点构成,外层黑线就是包含$X$的一个凸集,此时$conv(X)$就是图中的蓝线,就像一根橡皮筋那样. 且由任意多个凸集的交集是凸集可得$conv(X)$仍为凸集.

另外, 维基百科上对凸包有四种不同的定义:

包含$X$的(唯一的)最小凸集.
所有包含$X$的凸集的交集.
$X$中所有点的凸组合.
所有单形体的并集.

其中第一第二条定义好理解,第三条中的凸组合定义如下:

给定$x_{1},...,x_{m}$,凸组合为$\{\sum\limits_{i = 1}^m\alpha_{i}x_{i}$|$\alpha_{i}\ge 0,\sum\limits_{i = 1}^m\alpha_{i}=1\}$.

比如这张图中的点$P$是$x_{1},x_{2},x_{3}$的凸组合,点$Q$则不是:

至于第四条中的单形体指的是是将三角形或四面体概念推广到任意维的概念,具体来说,$k$单形体是一个$k$维多面体,它是$k+1$顶点的凸包,比如说下图就是一个正的3单形体,它是4个顶点的凸包:

那么此时第四条就可以这样理解,还是这张图为例,此时的单形体就是所有以黑点为顶点的三角形,并起来就是蓝线内部.

仿射包

仿射包(affine hull):

集合$X$的仿射包,指所有包含$X$的仿射集的交集,记作$aff(X)$.

这里的仿射集是指:

集合$M$称为是仿射的,如果它包含所有穿过满足$x,y\in M$且$x\neq y$条件的点对$x,y$的直线.

维基上对仿射包定义有三:

包含$X$的最小仿射集.
所有包含$X$的仿射集的交集.
所有$X$中元素的仿射组合,即$aff(X)=\{\sum\limits_{i = 1}^m \alpha_{i}x_{i}|\sum\limits_{i = 1}^m\alpha_{i}=1\}$.

打开维基查询仿射集,发现该词条被并入仿射空间,这是因为:具有仿射结构的集合就是一个仿射空间,故仿射集即仿射空间.

维基上对仿射空间及仿射结构有这样一段有意思的描述(可略过):

仿射空间:忘记原点之后剩余的矢量空间;在仿射空间中,点与点之间做差可以得到向量,点与向量做加法将得到另一个点,但是点与点之间不可以做加法.

仿射结构:想象一下,$Alice$知道某个点是真正的原点,但$Bob$认为另一点$p$是原点,现求两个向量$a$和$b$的和.$Bob$画出$p$到$a$和$p$到$b$的箭头,然后用平行四边形法则找到他认为的向量$a+b$,但是$Alice$知道他实际计算了$p+(a-p)+(b-p)$.

类似地,$Alice$和$Bob$可以计算向量$a$和$b$的线性组合,通常会得到不同的答案.但是,如果线性组合中系数的和为1,则$Alice$和$Bob$将得到相同的答案.

举个例子:如果爱丽丝计算$a$和$b$的线性组合,$\lambda a+(1-\lambda )b$,那么鲍勃可以得到相同的结果, $p+\lambda(a-p)+(1-\lambda)(b-p)=\lambda a+(1-\lambda)b$.

在这种情况下,尽管使用不同的原点,但对于所有系数$\lambda+(1-\lambda)=1$,$Alice$和$Bob$用相同的线性组合描述相同的点.

虽然$Alice$知道线性结构,但$Alice$和$Bob$都知道仿射结构,即仿射组合的值,定义为系数之和为1的线性组合.

非负组合

非负组合:

$X$中元素的非负组合为$\{\sum\limits_{i = 1}^m\alpha_{i}x_{i}|\alpha_{i}\ge 0\}$,正组合为$\{\sum\limits_{i = 1}^m\alpha_{i}x_{i}|\alpha_{i}> 0\}$.

显然和凸组合的定义相比,非负组合去除了$\sum\limits_{i = 1}^m\alpha_{i}=1$的限制.

由$X$生成的锥体(cone(X)):

由$X$生成的锥体,指$X$中所有元素的非负组合构成的集合,即$\{\sum\limits_{i = 1}^m\alpha_{i}x_{i}|\alpha_{i}\ge 0\}$,记作$cone(X)$.

注意与锥体定义的区别,锥体(cone):

$0\in X$,如果对 $\forall x \in X , \forall \lambda > 0, \lambda x \in X$ ,则称$X$为锥体.

Carathéodory定理

Carathéodory定理:

令$X$为$\mathbb{R}^{n}$中的一个非空子集. - 每个取自$X$生成的锥体$cone(X)$的非零向量都可以表示成$X$中线性无关向量的正组合. - 每个取自$X$的凸包$conv(X)$的向量都可以表示成$X$中不超过$n+1$个向量的凸组合.

第一条很显然,第二条还是参照下图,$\mathbb{R}^{n}$平面内,任意的蓝线内的点,总能找到$2+1$个点形成三角形,使点在该三角形内.

Carathéodory定理可以用来证明下述命题:

紧集的凸包是紧的.

证明略,有兴趣的朋友可以去读凸优化理论p21.

相对内点集与闭包

相对内点集

相对内点集:

令$C$为非空凸集,称$x$为$C$的相对内点,如果$x\in C$并且存在以$x$为中心的开球$S$,使得$aff(C)\cap S\subset C$,即$x$是相对于$C$的仿射包的内点.$C$的所有相对内点的集合称为$C$的相对内点集,并记作$ri(C)$.

集合$C$称为是相对开的,如果$ri(C)=C$.

闭包与相对边界点

闭包(Closure),维基上对其定义如下:

A set has closure under an operation if performance of that operation on members of the set always produces a member of the same set; in this case we also say that the set is closed under the operation.

比如欧氏空间$\mathbb{R}^{n}$中,集合$C$(未必是闭的)在取极限操作下有闭包$cl(C)$,意味着对$C$中收敛的点列取极限后得到的点仍在$cl(C)$中(对于不收敛的点列取极限为空,也可以说在$cl(C)$中).

记$cl(C)$为$C$的闭包,$cl(C)$中不是相对内点的点称为是$C$的相对边界点,这些点的集合称为是$C$的相对边界.

例如,令$C$为$R$上的$[a,b]$,则$aff(C)$则为$\mathbb{R}$,那么$ri(C)$则是$(a,b)$,$C$的相对边界则是$\{a,b\}$.特别的,若$C$本身是仿射集,那么此时$aff(C)=C=ri(C)$,相对边界是$\emptyset$.

相对内点的性质

线段原理

如下命题给出了相对内点的性质:

线段原理(Line Segment Principle):

$C$为非空凸集,如果$x\in ri(C)$,并且$y\in cl(C)$,那么连接两点$x,y$的线段上的点,除了$y$,都$\in ri(C)$.

相对内点的非空性

下述命题由线段原理推出:

相对内点的非空性:

令$C$为非空凸集.则

集合$C$的相对内点集$ri(C)$是非空凸集,并且和$C$具有相同的仿射包,即$aff(C)=aff(ri(C))$.

如果$C$的仿射包$aff(C)$的维数$m>0$的,那么必存在向量$x_{0},...,x_{m}\in ri(C)$,使得$x_{1}-x_{0},...,x_{m}-x_{0}$所张成的子空间平行于$aff(C)$.

这里$aff(C)$的维数定义为平行于$aff(C)$的子空间的维数.

延伸引理

另一有用结论同样可由线段原理得到:

延伸引理(Prolongation Lemma):

令$C$为非空凸集.$x\in ri(C)$,当且仅当对所有$y\in C$,存在$\gamma >0$,使得$x+\gamma (x-y)\in C$.

即$C$中以$x$为端点的所有线段可以延伸超过$x$而不必离开$C$.

相对内点与对偶理论

后面的章节中将看到相对内点的概念在凸优化和对偶理论中具有广泛应用,例如,当代价函数是凹的时,我们可以给出最后解集的一个刻画.

令$X$为$\mathbb{R}^{n}$中一个非空凸子集,且函数$f:X\mapsto R$为凹,$X^{+}$为使$f$在$X$上达到最小的向量集,即: $X^{+}=\{x^{+}\in X|f(x^{+})=\inf \limits_{x\in X}f(x)\}$.如果$X^{+}$包含$X$的相对内点,那么$f$在$X$上必为常数.

相对内点集与闭包的演算

为了研究凸集的集合运算,我们同样需要得到相应的相对内点集与闭包的运算结果,这里仅作概述(其中$C,C_{1},C_{2}$为非空凸集,$A$为线性变换):

两个凸集具有相同的$cl$当且仅当它们具有相同的$ri$.
$A•ri(C)=ri(A•C);A•cl(C)⊂cl(A•C)$且$C$有界时取等号.
特别的,$A$为$(x_{1},x_{2})$到$x_{1}+x_{2}$的线性变换时,有$ri(C_{1}+C_{2})=ri(C_{1})+ri(C_{2})$; $cl(C_{1}+C_{2})\subset cl(C_{1})+cl(C_{2})$且$C_{1},C_{2}$至少一个有界时取等号.
$ri(C_{1})\cap ri(C_{2})\subset ri(C_{1}\cap C_{2})$且$ri(C_{1})\cap ri(C_{2})\neq\emptyset$时取等号.
$cl(C_{1}\cap C_{2})\subset cl(C_{1})\cap cl(C_{2})$且$ri(C_{1})\cap ri(C_{2})\neq\emptyset$时取等号.
如果$A^{-1}•ri(C)$非空:$ri(A^{-1}•C)=A^{-1}•ri(C)$;$cl(A^{-1}•C)=A^{-1}•cl(C)$.

第二条说明闭凸集在线性变换下不一定是闭的,这是凸优化分析上存在困难的一个主要原因.

凸函数的连续性

凸函数有一个基本的性质:

凸函数的连续性:

如果$f:\mathbb{R}^{n}\mapsto \mathbb{R}$是凸的,那么它一定是连续的.更一般的,如果$f:\mathbb{R}^{n}\mapsto (-\infty,+\infty]$,那么限制在$dom(f)$上的函数$f$在$dom(f)$的相对内点集上是连续的.

该命题蕴含实值凸函数是连续的,进而是闭的($f$下半连续等价于$f$闭),对于单变量函数的情形,我们还有如下更强的结论:

如果$C$是$\mathbb{R}$上的一个闭区间,且$f:C\mapsto \mathbb{R}$是闭的和凸的,那么$f$在$C$上连续.

事实上,数学分析中关于凸函数有如下推论(斐礼文的数学分析中的典型问题与方法):

若$f$在区间$I$上凸,那么$f$在任意内点上连续.

那么利用上述推论或者利用凸函数的连续性,再加上$f$闭不难得出$f$在闭区间$C$连续.

函数的闭包

本节研究可以把给定函数变换为闭凸函数,同时又能保留该函数主要特性的运算.

$\mathbb{R}^{n+1}$的非空子集$E$是某个函数的上图,如果它满足:对每个点$(x,\omega)\in E$,集合$\{\omega|(x,\omega)\in E\}$要么是实数直线,要么是下方有界的半直线.

闭包

$f$的闭包(closure):

函数$f:X\mapsto [-\infty,+\infty]$的上图的闭包可以看做是另一个函数的上图.这个函数被称为是$f$的闭包,记作$clf$. $clf :\mathbb{R}^{n}\mapsto [-\infty,+\infty]$,且$(clf )(x)=\inf\{\omega|(x,\omega)\in cl(epi(f))\},\forall x\in \mathbb{R}^{n}$.

当$f$凸时,$epi(f)$凸,那么$cl(epi(f))$是闭的凸的(凸集的闭包仍凸).这意味着$clf $是闭的凸的,因为依据定义有$epi(clf)=cl(epi(f))$.

凸闭包

$f$的凸闭包(convex closure):

$f$的上图的凸包的闭包是某个函数的上图.这个函数被称为是$f$的凸闭包,记作$\hat{cl}f$, 令$F(x)=\inf\{\omega|(x,\omega)\in conv(epi(f))\},\forall x\in \mathbb{R}^{n}$,那么$\hat{cl}f$是函数$F$的闭包.

$F$是凸的,但它未必是闭的.$\hat{cl}f$ 是闭的凸的.

闭包的性质

从优化的角度看,下述命题叙述了一条重要性质,即$f$,$clf$ ,$F$和$\hat{cl}f$的最小值是一样的:

$f:X\mapsto [-\infty,+\infty]$为一函数,有\[\inf\limits_{x\in X}f(x)=\inf\limits_{x\in X}clf(x)=\inf\limits_{x\in \mathbb{R}^{n}}clf(x)=\inf\limits_{x\in \mathbb{R}^{n}}F(x)=\inf\limits_{x\in \mathbb{R}^{n}}\hat{cl}f(x)\]

下面的命题给出闭包的一个特性:

$f:X\mapsto [-\infty,+\infty]$为一函数,

$clf$是被$f$控制的最大闭函数.

$\hat{cl}f$是被$f$控制的最大闭凸函数.

这里被控制即如果$g$是闭的且$g\le f$,那么$g\le clf$.

研究凸函数的闭包是因为在某种意义下闭包与原函数差别最小.特别的,可以证明凸函数在它的定义域的相对内点集上与它的闭包一致:

$f:X\mapsto [-\infty,+\infty]$为一凸函数,则:

$cl(dom(f))=cl(dom(clf))$,$ri(dom(f))=ri(dom(clf))$

$(clf )(x)=f(x),\forall x\in ri(dom(f))$,$clf$是真的当且仅当$f$是真的.

如果$x\in ri(dom(f))$,我们有:$(clf)(y)=\lim\limits_{\alpha\downarrow 0}f(y+\alpha (x-y)),\forall y\in \mathbb{R}^{n}$.

下面两个命题是刻画凸函数经过线性变换之后所得函数的闭包:

$f:X\mapsto [-\infty,+\infty]$为一凸函数,且A为一$m×n$矩阵使得A的值域包含$ri(dom(f))$中的一个点.那么由 $F(x)=f(Ax)$定义的函数$F$是凸的,并且\[(clF)(x)=(clf)(Ax),\forall x\in \mathbb{R}^{n}\]

下述命题本质上式上述命题的一个特例:

$f_{i}:\mathbb{R}^{n}\mapsto [-\infty,+\infty],i=1,...,m$,为凸函数,且$\cap_{i=1,...,m}ri(dom(f_{i}))\neq\emptyset$.那么由$F(x)=f_{1}(x)+...+f_{m}(x)$定义的函数$F$是凸的,并且\[(clF)(x)=(clf_{m})(x)+...+(clf_{m})(x),\forall x\in \mathbb{R}^{n}\]

回收锥

回收锥与线形空间

回收锥

回收方向

回收方向(direction of recession):

给定非空凸集$C$,我们说$d$是$C$的一个回收方向,如果$x+\alpha d\in C$对所有的$x$属于$C$和$\alpha\ge 0$都成立.

通俗的解释就是我们从$C$中任意点出发,沿着$d$的方向走到无穷,而永远不穿过$C$的相对边界点跑到$C$之外.

回收锥

回收锥(recession cone):

所有回收方向的集合是一个包含原点的锥体.称之为$C$的回收锥,记作$R_{C}$.

闭凸集的一条重要性质就是为检验$d\in R_{C}$是否成立,只需验证$x+\alpha d\in C$对单一的$x\in C$成立就可以了.这就是下述命题的下半部分.

回收锥定理

回收锥定理(Recession Cone Theorem):

$C$为非空闭凸集.

回收锥$R_{C}$是闭的凸的.

向量$d\in R_{C}$当且仅当存在向量$x\in C$使得$x+\alpha d\in C$对所有的$\alpha\ge 0$成立.

回收锥的性质

下述命题给出回收锥的一些其他性质.

$C$为非空闭凸集.

$R_{C}$包含一个非零的方向当且仅当$C$是无界的.

$R_{C}$=$R_{ri(C)}$.

对任意一组闭凸集$C_{i},i\in I$,并且$\cap_{i\in I}C_{i}\neq\emptyset$,有$R_{\cap_{i\in I}C_{i}}=\cap_{i\in I}R_{C_{i}}$.

$W$为$\mathbb{R}^{m}$的紧的凸子集,并令$A$为一$m×n$矩阵.集合$V=\{x\in C|Ax\in W\}$的回收锥是$R_{C}\cap N(A)$,其中$N(A)$是$A$的零空间(nullspace).

线形空间

凸集$C$的回收锥有一个重要子集,称为其线形空间(lineality space),

线形空间,记作$L_{C}$,定义为$-d$也是回收方向的方向$d$的集合:$L_{C}=R_{C}\cap (-R_{C})$.

因此$d\in L_{C}$当且仅当整个直线$\{x+\alpha d|\alpha\in R\}$对于每个$x\in C$都包含于$C$中.

线形空间的性质

线形空间仍然有我们已经有的回收锥的若干性质:

$C$为$\mathbb{R}^{n}$的非空闭凸集.

$L_{C}$是$\mathbb{R}^{n}$的子空间.

$L_{C}=L_{ri(C)}$.

对任意一组闭凸集$C_{i},i\in I$,并且$\cap_{i\in I}C_{i}\neq\emptyset$,有$L_{\cap_{i\in I}C_{i}}=\cap_{i\in I}L_{C_{i}}$.

$W$为$\mathbb{R}^{m}$的紧的凸子集,并令$A$为一$m×n$矩阵.集合$V=\{x\in C|Ax\in W\}$的线形空间是$L_{C}\cap N(A)$,其中$N(A)$是$A$的零空间(nullspace).

回收锥与线形空间的一个例子

举例来说,考虑集合$C=\{x|x'Qx+c'x+b\le 0\}$,$Q$为对称正定的$n$维方阵,$c$为$n$维向量. 向量$d$是回收方向当且仅当$(x+\alpha d)'Q(x+\alpha d)+c'(x+\alpha d)+b\le 0,\forall\alpha>0$.显然不可能有$d'Qd>0$,所以只能$d'Qd=0$,又$Q$半正定,故存在$M$,$s.t.Q=M'M$,这使得$Md=0$,这表明$Qd=M'Md=0$.故原式等价于$x'Qx+c'x+b+\alpha c'd\le0,\forall\alpha>0$.而此式成立当且仅当$c'd\le 0$.于是: \[R_{C}=\{d|Qd=0,c'd≤0\}$;$L_{C}=\{d|Qd=0,c'd=0\}\]

凸集分解

最后是一个有用的结论,它使得我们可以吧凸集按照它的线形空间(的子空间)和它的正交补进行分解:

凸集分解:

$C$为$\mathbb{R}^{n}$的非空闭凸集.则对于每个包含在线形空间$L_{C}$中的子空间$S$,我们都有:$C=S+(C+S_{\perp})$.

凸函数的回收方向与不变空间

与上节对应的,函数中也有类似的概念. 这个概念的重要性在于凸优化问题解得存在性.$epi(f)$回收锥的方向可以得到$f$不单调增加的方向.

凸函数的回收方向

$f:\mathbb{R}^{n}\mapsto (-\infty,+\infty]$为闭的真凸函数,考虑水平集$V_{\gamma},\gamma\in R$.则:

所有的非空水平集$V_{\gamma}$都具有相同的回收锥,记作$R_{f}$,由$R_{f}=\{d|(d,0)\in R_{epi(f)}\}$给出.

如果某个非空水平集$V_{\gamma}$是紧的,那么所有这些水平集都是紧的.

$f$的回收方向:

向量$d\in R_{f}$称为$f$的回收方向,其中$R_{f}$由$R_{f}=\{d|(d,0)\in R_{epi(f)}\}$给出.

一个直观的理解就是f的回收方向是对f连续不升的方向,反之,如果我们从某个$x\in dom(f)$出发,而且在沿着方向$d$移动时,我们遇到点$z$满足$f(z)>f(x)$,那么$d$不可能称为回收方向.由$f$的水平集的凸性,一旦我们跨过水平集的相对边界,我们将永远不会再次跨过该边界,而且,一个方向若不是$f$的回收方向,其将最终为$f$连续上升的方向.

凸函数的不变空间

闭的真凸函数$f$的回收锥$R_{f}$的线形空间记为$L_{f}$.它是由$d$和$-d$都是$f$的回收方向的所有$d$构成子空间,即$L_{f}=R_{f}∩(-R_{f})$.

$f$的不变空间(constancy space):

向量$d\in L_{f}$称为让$f$常值的方向,而$L_{f}=R_{f}∩(-R_{f})$称为$f$的不变空间.

举例来说,如果$f(x)=x'Qx+c'x+b$为二次函数,$Q$为对称正定的$n$维方阵,$c$为$n$维向量,那么它的回收锥和不变空间是: $R_{f}=\{d|Qd=0,c'd\le 0\};L_{f}=\{d|Qd=0,c'd=0\}$.

回收函数

我们已经有,如果$d$是f的回收方向,那么$f$沿着射线$x+\alpha d$是渐进非增的,但事实上我们有更强的性质,$f$沿着$d$的渐进斜率独立于起点$x$.现在引入一个函数表示闭的真凸函数沿着某个方向的渐进斜率,即回收函数:

$r_{f}$称为是$f$的回收函数,如果满足$epi(r_{f})=R_{epi(f)}$.

注意到$R_{epi(f)}$是另外一个闭的真凸函数的上图,即$r_{f}$是闭的真凸函数.

刻画凸函数的回收锥和不变空间

回收函数$r_{f}$可以用来刻画凸函数的回收锥和不变空间.

$f:\mathbb{R}^{n}\mapsto (-\infty,+\infty]$为闭的真凸函数.则$f$的回收锥和不变函数可以用它的回收函数给出:\[R_{f}=\{d|r_{f}(d)\le 0\}, L_{f}=\{d|r_{f}(d)=r_{f}(-d)=0\}\]

$d$是$f$的回收方向,那么$f$沿着射线$x+\alpha d$是渐进非增的,即$r_{f}(d)\le 0$,这就是上文中渐进斜率的含义.下述命题给出了回收函数的显示表达:

$f:\mathbb{R}^{n}\mapsto (-\infty,+\infty]$为闭的真凸函数.则对于所有的$x\in dom(f)$和$d\in \mathbb{R}^{n}$, \[r_{f}(d)=\sup\limits_{\alpha>0}(f(x+\alpha d)-f(x))/\alpha=\lim\limits_{\alpha\to +\infty}(f(x+\alpha d)-f(x))/\alpha\]

最后是和的回收函数:

$f_{i}:\mathbb{R}^{n}\mapsto (-\infty,+\infty],i=1,...,m$,为闭的真凸函数,且$f=f_{1}+...+f_{m}$为真.则\[r_{f}(d)=r_{f_{1}}(d)+...+r_{f_{m}}(d),\forall d\in \mathbb{R}^{n}\]

闭集交的非空性与线性变换下的闭性

闭集交的非空性

回收锥与线形空间的概念可以用来把紧集合的某些性质推广到闭凸集上去:

嵌套的非空闭集$\{C_{k}\}$具有非空紧交集.
紧集在线性变换下是紧的.

考虑$\mathbb{R}^{n}$中嵌套的非空闭集$\{C_{k}\}$,满足有$C_{k+1}⊂C_{k}$,证明$\cap_{k=0,...,+\infty}C_{k}$是否为空的问题会在以下背景中出现:

函数$f:\mathbb{R}^{n}\mapsto\mathbb{R}$在集合$X$上是否会达到最小值?该问题的答案为当且仅当$\cap^{\infty}_{k=0}\{x\in X|f(x)\le\gamma_{k}\}$非空,其中$\gamma_{k}\downarrow\inf_{x\in X}f(x)$.
如果$C$是闭集,$A$是矩阵,$AC$是否为闭集?令$\{y_{k}\}\to y$为$AC$中一个收敛的序列,接着证$y\in AC$.一种方法是引入集合$C_{k}=C\cap N_{k}$,其中$N_{k}=\{x|║Ax-y║\le║y_{k}-y║\}$,那么一个充分条件就是\[\cap_{k=0,...,+\infty}C_{k}\neq\emptyset\]

一个重要的事实是$\cap_{k=0,...,+\infty}C_{k}$为空当且仅当$\{C_{k}\}$中的序列$\{x_{k}\}$都是无界的.因此我们的思路是引入保证并非所有这样的序列都是无界的,事实上只要关心如下定义中沿着公共方向发散到$+\infty$的无界序列就可以了.

渐进序列:

$\{C_{k}\}$为嵌套的非空闭凸集序列,我们说$\{x_{k}\}$是$\{C_{k}\}$的一个渐进序列,如果$x_{k}\neq0$,$x_{k}\in C_{k}$对所有的$k$成立,并且\[║x_{k}║\to+\infty,x_{k}/║x_{k}║→d/║d║\]其中$d\in\cap_{k=0,...,+∞}R_{C_{k}}$是公共非零回收方向.

下面引入具有我们所期望性质的一类序列.

收缩的(retractive):

$\{C_{k}\}$为嵌套的非空闭凸集序列,我们说$\{x_{k}\}$为收缩的,如果对上述渐进序列的定义中对应于$\{x_{k}\}$的方向$d$,存在下标$\bar{k}$,使得$x_{k}-d\in C_{k},\forall k\ge \bar{k}$.

我们称$\{C_{k}\}$是收缩的,如果它的所有渐进序列都是收缩的.下图形象的说明了收缩这一概念,显然$(a)$是收缩的而$(b)$不是.

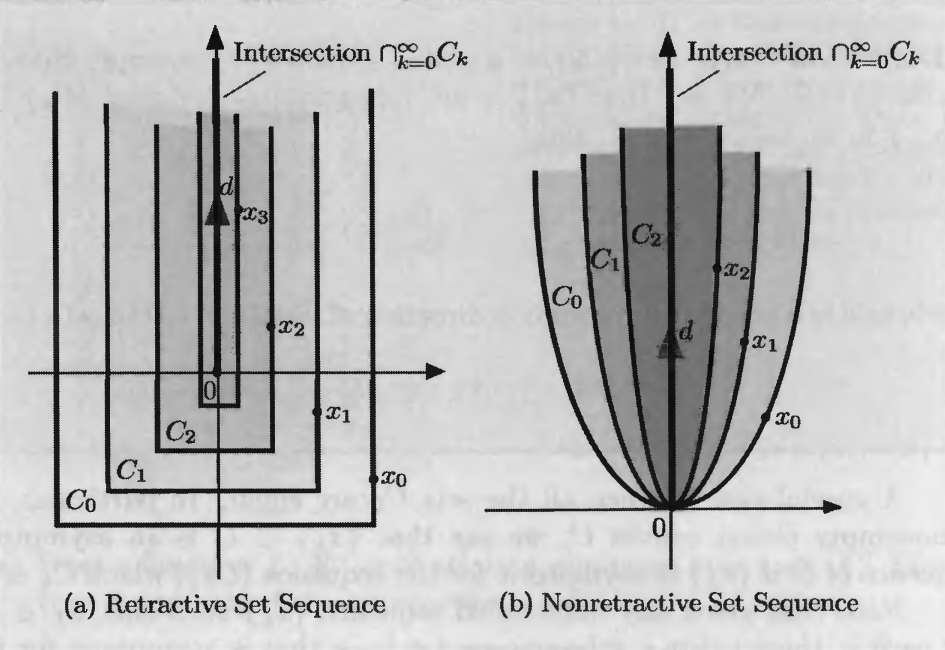
多面体集合是最重要的一类收缩集:

多面体集合是收缩的.

收缩序列的重要性可从如下命题中看出:

收缩的嵌套非空闭凸集序列具有非空交集.

上述命题适用的一个简单例子就是圆柱形集合序列,其中$R_{C_{k}}=L_{C_{k}}=L$.下面命题给出了一个重要的拓展结果:

$\{C_{k}\}$为非空闭凸集序列,记$R=\cap_{k=0,...,+\infty}R_{C_{k}},L=\cap_{k=0,...,+\infty}L_{C_{k}}$.

如果$R=L$,那么$\{C_{k}\}$是收缩的,且$\cap_{k=0,...,+\infty}C_{k}\neq\emptyset$,进而$\cap_{k=0,...,+\infty}C_{k}=L+\hat{C}$,其中$\hat{C}$为一非空紧集.

$X$为收缩的闭凸集,假定所有集合$\bar{C_{k}}=X\cap C_{k}\neq\emptyset$,且$R_{X}\cap R\subset L$,则$\{\bar{C_{k}}\}$是收缩的,且$\cap_{k=0,...,+\infty}\bar{C_{k}}\neq\emptyset$.

下面是一个重要应用:

凸二次规划解的存在性:

令$Q$为对称半正定$n$阶方阵,$c$和$a_{1},...,a_{r}$为$n$维向量,$b_{1},...,b_{r}$为标量,假定优化问题:\[minx'Qx+c'x\] \[s.t.a'_{j}x\le b_{j},j=1,...,r\]的最优值为有限,则该问题至少有一个最优解.

线性变换下的闭性

上节得到的闭凸集序列交的非空性可以转化为保证闭凸集$C$在线性变换$A$下的像$AC$的闭性条件,这就是下述命题:

$X$和$C$为$\mathbb{R}^{n}$中的非空闭集,$A$为$m×n$矩阵,且记$N(A)$为其零化空间.如果$X$是收缩的闭凸集且$R_{X}\cap R_{C}\cap N(A)\subset L_{C}$,那么$A(X\cap C)$为闭集.

令$C=\mathbb{R}^{n}$,$X$为多面体集,则$L_{C}=\mathbb{R}^{n}$,上述命题条件自动满足,于是$AX$为闭,因此多面体集在线性变换下的像为闭集.

令$X=\mathbb{R}^{n}$,则如果$C$的每个属于$N(A)$的回收方向都属于$L_{C}$,那么$AC$闭.特别的,$R_{C}\cap N(A)={0}$时必然成立.

作为特例,该结果可以用来得到保证闭凸集向量和的闭性的条件.

$C_{1},...,C_{m}$为$\mathbb{R}^{n}$中的非空闭凸子集,假定等式$d_{1}+...+d_{m}=0$对某些向量$d_{i}\in R_{C_{i}}$成立就意味着$d_{i}\in L_{C_{i}}$对所有$i=1,...,m$成立.则$C_{1}+...+C_{m}$是闭集.

特别的取$m=2$,且$C_{1},C_{2}$有界,显然$R_{C_{1}}=R_{C_{2}}={0}$,此时条件自动成立,那么$C_{1}+C_{2}$为闭集.

超平面

分离超平面

超平面:

超平面是$\mathbb{R}^{n}$中形如$\{x|a'x=b\}$的集合,其中$a$是$n$维向量,$b$为标量.

任取超平面内的向量都满足$a'\bar x=b$,所以该超平面亦可被等价定义为$H=\{x|a'x=a'\bar x\}$或$H=\bar x+\{x|a'x=0\}$,$a$被称为$H$的法向量.

集合$\{x|a'x\ge b\}$与$\{x|a'x\le b\}$被称为与超平面关联的闭半空间,两者也分别被称为正、负半空间. 集合$\{x|a'x> b\}$与$\{x|a'x< b\}$则被称为与超平面关联的开半空间.

分离:

称集合$C_{1}$,$C_{2}$是可被超平面$\{x|a'x=b\}$分离的,如果两个集合分别被包含于与H关联的两个闭半空间内,也即满足:$a'x_{1}\le b\le a'x_{2},\forall x_{1}\in C_{1},\forall x_{2}\in C_{2}$成立.

支撑:

在集合$C$的闭包内任取向量$\bar x$如果一超平面能将$C$与单点集{$\bar x$}分离,则称该超平面在$\bar x$上支撑$C$.即存在非零向量$a$使得$a'\bar x\le a'x,\forall x\in C$.

等价的,由于$\bar x$是$C$的闭包点(closure point),所以$a'\bar x=\inf \limits_{x\in C}a'x$.

支撑超平面定理(Supporting Hyperplane Theorem):

$C$为$\mathbb{R}^{n}$中的非空凸子集,$\bar x$为$\mathbb{R}^{n}$中向量,如果$\bar x$不是$C$的内点,则存在通过$\bar x$的超平面使得$C$包含于其某个闭半空间内,也即存在向量$a\neq 0$使得$a'\bar x\le a'x,\forall x\in C$.

分离超平面定理:

$C_{1}$与$C_{2}$为$\mathbb{R}^{n}$中的非空凸子集,如果$C_{1}$与$C_{2}$不交(disjoint),则存在分离超平面.即存在非零向量$a$使得$a'x_{1}\le a'x_{2},\forall x_{1}\in C_{1},\forall x_{2}\in C_{2}$.

严格分离(strictly separate):

称超平面$\{x|a'x=b\}$严格分离$C_{1}$与$C_{2}$,如果其不仅能分离$C_{1}$与$C_{2}$,还与两个集合都没有交点,即$a'x_{1}< b< a'x_{2},\forall x_{1}\in C_{1},\forall x_{2}\in C_{2}$或$a'x_{2}< b< a'x_{1},\forall x_{1}\in C_{1},\forall x_{2}\in C_{2}$成立.

严格分离定理:

$C_{1}$与$C_{2}$为$\mathbb{R}^{n}$中的非空凸子集,且$C_{1}$与$C_{2}$不交(disjoint),当下列任一条件满足时,$C_{1}$与$C_{2}$能被严格分离.

$C_{2}-C_{1}$是闭集.

$C_{1}$是闭集且$C_{2}$是紧集.

$C_{1}$与$C_{2}$都是多面体.

$C_{1}$与$C_{2}$都是闭集且满足$R_{C_{1}}\cap R_{C_{2}}=L_{C_{1}}\cap L_{C_{2}}$.

$C_{1}$是闭集,$C_{2}$是多面体且满足$R_{C_{1}}\cap R_{C_{2}}\subset L_{C_{1}}$.

上述结论的一个推论是,闭集$C$与任何不属于$C$的向量$\bar x$总可以被严格分离.根据这个性质,可以得到闭凸集如下重要性质:

集合$C$的凸包是包含$C$的所有闭半空间的交集.特别的,一个闭凸集是包含它的所有闭半空间的交集.

真分离超平面

真分离(proper separate):

称超平面$\{x|a'x=b\}$真分离$C_{1}$与$C_{2}$,如果其不仅分离$C_{1}$与$C_{2}$且不同时包含$C_{1}$与$C_{2}$.即\[\sup \limits _ {x_{1}\in C_{1}} a'x_{1} \le \inf \limits _ {x_{2}\in C_{2}} a'x_{2} ,\inf \limits _ {x_{1}\in C_{1}} a'x_{1} < \sup \limits _ {x_{2}\in C_{2}} a'x_{2}\]

下证严格分离>分离,真分离>分离: 由定义,显然有严格分离$\ge$分离,真分离$\ge$分离. 想象$\mathbb{R}^{2}$空间中$C_{1}=\{(x,y)|x\in [0,2],y=0\}$和$C_{2}=\{(x,y)|x\in [1,3],y=0\}$,显然$C_{1}$与$C_{2}$为凸集,$\{(x,y)|y=0\}$能够分离$C_{1}$与$C_{2}$,但不能真分离或是严格分离$C_{1}$与$C_{2}$.即有严格分离>分离,真分离>分离.

真分离定理:

$C$为$\mathbb{R}^{n}$中的非空凸子集,$\bar x$为$\mathbb{R}^{n}$中向量,当且仅当$\bar x\notin ri(C)$时,存在$C$与$\bar x$的真分离超平面.

两个凸集的真分离定理:

$C_{1}$与$C_{2}$为$\mathbb{R}^{n}$中的非空凸子集,则其存在真分离超平面当且仅当$ri(C_{1})\cap ri(C_{2})=\emptyset$.

多面体的真分离定理:

$C$与$P$是$\mathbb{R}^{n}$中的非空凸子集且$P$是多面体.则存在分离$C$与$P$且其不包含$C$的超平面存在当且仅当$ri(C)\cap P=\emptyset$.

非竖直超平面

在优化问题中,常常用支撑超平面来分析函数的上图,对于定义在$\mathbb{R}^{n}$上的函数,其上图是$\mathbb{R}^{n+1}$的子集,此时考虑$\mathbb{R}^{n+1}$中的超平面,并将其法向量记为$(\mu,\beta)$的n+1维向量,其中$\mu\in \mathbb{R}^{n}$而$\beta\in \mathbb{R}$,如果$\beta=0$,称该超平面是竖直的(vertical).

非竖直超平面定理:

$C$为$\mathbb{R}^{n+1}$中的非空凸子集,且$C$不包含任何直线,标记$\mathbb{R}^{n+1}$中的向量为$(u,w)$,其中$u\in \mathbb{R}^{n}$而$w\in \mathbb{R}$,则有:

存在非竖直超平面,使得其关联的闭半空间包含$C$,也即存在向量$\mu\in \mathbb{R}^{n}$,标量$\beta\neq 0$,及标量$\gamma$使成立:$\mu'u+\beta w\ge \gamma$.

如果向量$(\bar u,\bar w)\notin cl(C)$,则存在非竖直超平面使得$(\bar u,\bar w)$与$C$严格分离.

共轭函数

最后一节介绍凸优化中一个基本概念叫函数的共轭变换(conjugate transformation),它有另外一个名字:Legendre–Fenchel transformation.

共轭函数

共轭函数(conjugate function):

扩充的实值函数$f:\mathbb{R}^{n}\mapsto[-\infty,+\infty]$,其共轭函数$f^{+}:\mathbb{R}^{n}\mapsto[-\infty,+\infty]$如下定义:\[f^{+}(y)=\sup \limits _ {x\in \mathbb{R}^{n}}\{x'y-f(x)\},\forall y\in \mathbb{R}^{n}\]

值得注意的是,无论$f$是否为凸函数,其共轭函数$f^{+}$总是闭凸函数,因为仿射函数族$x'y-f(x),\forall x\in dom(f)$处处收敛到$f^{+}$,也即$f^{+}$是它们的上确界.还需注意的是,无论$f$是否为真函数,$f^{+}$都不一定是真函数.

双重共轭函数

双重共轭函数(double conjugate):

考虑共轭函数$f^{+}$的共轭函数,记作$f^{+ +}$.

共轭定理

共轭定理:

$f^{+}$为函数$f:\mathbb{R}^{n}\mapsto[-\infty,+\infty]$的共轭函数,$f^{++}$为对应双重共轭函数.则有:

恒有$f(x)\ge f^{++}(x),\forall x\in \mathbb{R}^{n}$.

如果$f$是凸函数,则如果$f,f^{+},f^{++}$中有任一函数是真函数,则另外两个也是真函数.

如果$f$是真的闭凸函数,则$f=f^{++}$.

$f^{++}$与凸闭包函数$\hat{cl}f$相等,此外,如果$\hat{cl}f$是真函数,则$\hat{cl}f=f^{++}$.

上述定理不难看出共轭函数与凸闭包函数的相似之处,不同的是共轭函数完全通过非竖直超平面定义的,而图闭包函数的定义既用到了非竖直超平面,也用到了竖直超平面.

两个例子

例1(示性/支撑函数的共轭): 非空集合$X$示性函数(indicator function)的定义如下:\[\delta_{X}(x)=0,x\in X\]而$\delta_{X}(x)$的共轭函数:\[\sigma_{X}(x)=\sup \limits _ {x\in X} y'x\]并称为X的支撑函数.由共轭定理第四条,$X,cl(X),conv(X),cl(conv(X))$有相同的支撑函数.

例2(锥的支撑函数): $C$为凸锥,根据例1,C的示性函数$\delta_{C}$的共轭即$C$的支撑函数\[\sigma_{C}(y)=\sup \limits _ {x\in C} y'x\]由于$C$是锥体,可得:\[\sigma_{C}(y)=0,y'x\le 0,\forall x \in C;\infty,otherwise\]因此支撑函数$\sigma_{C}$恰为如下锥$C^{+}$的示性函数$\delta_{C^{+}}$,\[C^{+}=\{y|y'x\le 0,\forall x \in C\}\]称$C^{+}$为$C$的极锥(polar cone). 最后是常见的函数的共轭变换: