前言:本文主要是关于机器学习中的贝叶斯思想的一些简单认识, 主要参考了Coursera上国立高等经济大学Advanced Machine Learning系列课程Course3: Bayesian Methods for Machine Learning Week1.
引言
我们先来直观感受一下贝叶斯思想, 首先来看一道选择题, 在灭霸还没有诞生的时间节点, 纽约街头有一人在跑步, 你觉得?
- 他看到了灭霸.
- 他想跑步就跑了.
- 他一直喜欢跑步.
答案是B. 事实上, 使用先验信息可以排除A, 而C做了额外的假设. A.B.C.分别对应贝叶斯三条原则:
- 使用先验信息.
- 选择最能解释现象的答案.
- 避免做出额外的假设.
希望你们喜欢这道选择题,下面进入正题, 本文的主角是机器学习, 所以符号的选取会尽可能的采用机器学习中的惯用符号.
贝叶斯学派与频率学派
贝叶斯学派与频率学派是统计学的两大学派, 他们主要有如下两大不同:
- 贝叶斯学派将参数\(\theta\)视为变量, 数据\(X\)固定; 频率学派将参数\(\theta\)固定, 数据\(X\)视为变量.
- 贝叶斯学派: 得到关于参数的分布\(P(\theta\mid X)\); 频率学派: 得到参数值\(\hat{\theta}=\arg\max_{\theta}P(X\mid \theta)\)
贝叶斯思想最大的特点就是把参数\(\theta\)视为变量, 所以得到的结果也是关于参数\(\theta\)的分布, 更加一般化. 若要向得到参数值, 最简单的可以对后验分布求概率值最大的点(maximum a posterior):\[\theta_{MAP}=\arg\max_{\theta}P(\theta\mid X)\]
贝叶斯公式
贝叶斯公式想必大家都熟悉\[P(\theta\mid X)=\frac{P(X,\theta)}{P(X)}={\frac {P(X\mid \theta)\,P(\theta)}{P(X)}}\]其中\(P(\theta)\)称为先验分布, \(P(X\mid \theta)\)称为似然函数, 或者理解为模型, \(X\)为所得到的数据集, 或者说evidence, \(P(\theta\mid X)\)称为后验分布.
简单举两个例子说明贝叶斯公式在机器学习中的应用:
- 在线学习做的就是用数据\(X\)对\(P(\theta)\)进行更新得到\(P(\theta\mid X)\), 因为不知道新的样本到达时间, 所以基本上就是每来一个样本\(x_k\)就对参数进行一次更新: \[P_k(\theta)=P(\theta\mid x_k)=\frac {P(x_k\mid \theta)\,P_{k-1}(\theta)}{P(x_k)}\]比方说假定模型满足正态分布\(P(x\mid \theta)= N(\theta, 1)= \frac{1}{\sqrt{2\pi}} e^{-\frac{(x-\theta)^2}{2}}\), 假定先验\(P_0(\theta)=N(0,1)\), 将数据\(x_1=1\)喂给它, 容易得到\[P_1(\theta)=\frac{1}{2\pi} e^{-\frac{(1-\theta)^2}{2}} e^{-\frac{\theta^2}{2}}/P(x_k)\propto N(\frac{1}{2},\frac{1}{2}) \]注意到\(P(x_k)\)与\(\theta\)无关所以不在乎,另外容易看到\(\theta\)的后验的期望向1迈出了一步.
- 将贝叶斯公式应用到监督学习中,记参数为\(\omega\): \[P(\omega\mid X, y)=\frac {P(\omega, y\mid X)}{P(y\mid X)}=\frac {P(y\mid X, \omega)\,P(\omega)}{P(y\mid X)}\]其中\(P(y\mid X, \omega)\)为模型的基本结构,比方说\(P(y\mid X, \omega)=N(X\omega, \sigma^2 I)\), 协方差阵固定位单位阵的倍数, 这实际上假定了样本之间的独立性, 若还假定参数\(\omega\)满足正态分布, 则在线性模型中可以得到最小二乘法加L2正则项的结果(下文会加以详细说明). 有了模型\(P(y\mid X, \omega)\)和参数\(P(\omega\mid X, y)\), 我们可以通过下式在测试集上进行预测:\[P(y_{test}\mid X_{test}, X ,y)=\int P(y_{test}\mid X_{test}, \omega)P(\omega\mid X, y) d\omega\]
有了上述两个例子, 想必大家都有了自己的理解, 在机器学习中, 模型\(P(y\mid X, \omega)\)的选取与先验\(P(\omega)\)成为了两个最关键的要素, 而模型\(P(y\mid X, \omega)\)的选取是我们首先要考虑的,下面来看:
如何定义一个模型
一般的监督学习任务, 我们所有的是一堆互相相关的特征, 目标是试图从中找出一些因果关系, 一个自然地想法就是试图用一些箭头来表示这种因果关系, 图片来自贝叶斯网络的维基百科: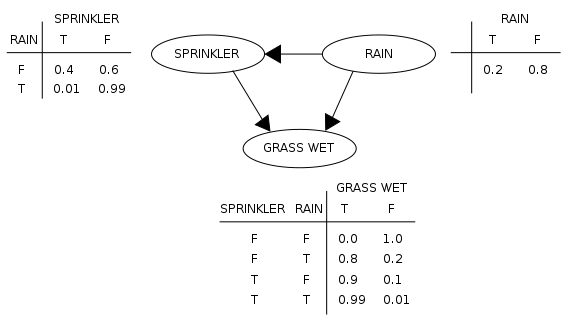
这里我们关心这样一个问题,看到草坪湿了, 想知道有没有下过雨. 由常识容易知道:下雨能导致草坪湿掉, 喷洒器也能导致草坪湿掉, 且下雨天喷洒器往往不会运作, 有了这张图, 我们也就能轻易的表示出\(P(Rain\mid Grass)\), 这样的有向非循环的图模型被称为是贝叶斯网络.
再来看一个贝叶斯网络的简单例子:贝叶斯分类器, 图片来自周志华的机器学习: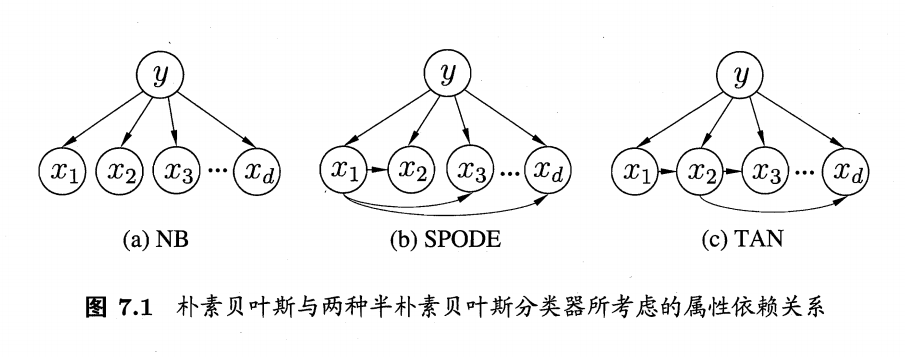
(a)是朴素贝叶斯, 想法也非常朴素, 特征\(x_i\)仅仅由\(y\)所决定, (b)、(c)则是考虑了特征之间的依赖关系.
这里提一下板表示法, 板表示法(plate notation)是一种表示在图形模型中重复的变量的方法, 比方说朴素贝叶斯分类器(a)可以简画为: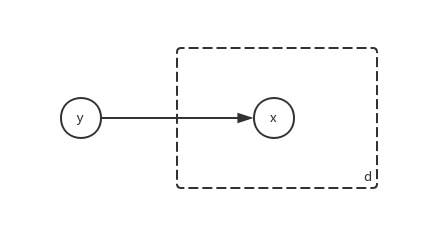
图中的d表示将方形区域重复d遍, 也就是(a)中图形的样子. 模型的选取先说这么多, 下面考虑先验\(P(\omega)\)的选取, 事实上, 为了计算简单, 一般选取共轭先验分布.
共轭先验
关于贝叶斯公式,还有一个重要概念:共轭先验, 是指先验分布和后验分布同属某个分布的先验分布,这里举三个重要的共轭先验的例子:
- 假定模型满足正态分布\(P(X\mid \theta)= N(\theta, \sigma^2)\), 其中\(\sigma^2\)为给定值. 给定先验\(P(\theta)= N(0, 1)\)满足标准正态分布. 此时后验分布:\[ P(\theta\mid X) \propto e^{-\frac{(x-\theta)^2}{2\sigma^2}} e^{-\frac{\theta^2}{2}}\propto N(\frac{x}{1+\sigma^2}, \frac{\sigma^2}{1+\sigma^2})\]这个例子实际上在贝叶斯公式一节中讲到了,不难发现,若喂给它的数据是\(x=0\), 那么\(\theta\)的后验分布第一个参数不变,第二根参数减小了些,也即期望值不变,方差减小了些.
- 假定模型满足正态分布\(P(X\mid \gamma)=N(\mu, \gamma^{-1})\), 其中\(\mu\)为给定值,\(\gamma=\frac{1}{\sigma^2}\)称为准确度,方差越小,准确度越高.给定先验\(P(\gamma)= \Gamma(a,b)\propto\gamma^{a-1}e^{-b\gamma}\)满足参数为\(a,b\)的Gamma分布.此时后验分布:\[ P(\gamma\mid X) \propto \gamma^{\frac{1}{2}+a-1} e^{-(b+\frac{(x-\mu)^2}{2})\gamma} \propto \Gamma(\frac{1}{2}+a, b+\frac{(x-\mu)^2}{2})\]不难发现,若喂给它的数据是\(x=\mu\), 那么\(\gamma\)的后验分布第一个参数增大了\(\frac{1}{2}\),第二个参数不变,注意到Gamma分布的期望\(E[\Gamma(a,b)]=\frac{a}{b}\), 也即准确度\(\gamma\)的期望变大了些, 若一直喂给它相同的数据\(x=\mu\), 可以看到准确度\(\gamma\)的期望会一直上涨, 这也与我们的想象相符合.
- 假定模型满足二项分布\(P(X\mid \theta)= \theta^x(1-\theta)^{(1-x)}\). 给定先验\(P(\theta)=Be(a,b) \propto\theta^{a-1}(1-\theta)^{b-1}\)满足参数为\(a,b\)的Beta分布.此时后验分布:\[ P(\theta\mid X) \propto \theta^{x+a-1}(1-\theta)^{1-x+b-1} \propto Be(x+a, 1-x+b)\]若喂给它的数据是\(x=1\), 那么\(\theta\)的后验分布第一个参数增大了\(1\),第二个参数不变,注意到Beta分布的期望\(E[Be(a,b)]=\frac{a}{a+b}\), 也即\(\theta\)的期望向\(1\)迈出了一小步, 这也与我们的想象相符.
贝叶斯视角下的线性回归与最小二乘线性回归
考虑线性回归模型\(y=X\omega\), 这里的\(y\)为\(m\)维列向量, \(\omega\)为\(n\)维列向量, 假定模型满足正态分布\(P(y\mid X, \omega)=N(X\omega, \sigma^2I)\), 先验也满足正态分布\(P(\omega)=N(0, \gamma^2I)\), 容易得到:\[P(\omega\mid X, y)=\frac {P(\omega, y\mid X)}{P(y\mid X)}=\frac {P(y\mid X, \omega)\,P(\omega)}{P(y\mid X)}\propto e^{-\frac{1}{2\sigma^2}(y-X\omega)^T(y-X\omega)}e^{-\frac{1}{2\gamma^2}\omega^T\omega}\]可以通过PRML一书2.3.3节最后的公式给出后验的正态分布的参数, 这里仅求该后验分布的概率最大值点: \(\omega_{MAP}=\arg\max_{\omega}P(\omega\mid X, y)\), 易知取\(\log\)不影响求最大值:\[\log P(\omega\mid X, y)=-\frac{1}{2\sigma^2}(y-X\omega)^T(y-X\omega)-\frac{1}{2\gamma^2}\omega^T\omega=-\frac{1}{2\sigma^2}(\left\Vert y-X\omega\right\Vert^2+\frac{\sigma^2}{\gamma^2}\left\Vert \omega\right\Vert^2)\]对其求最大值即为最小二乘方法加L2正则项的结果. 如果有兴趣, 不妨将上面对\(\omega\)的先验分布替换成参数为\(0,b\)的拉普拉斯分布\(P(\omega)=\frac{1}{(2b)^n} \prod_ {i=1}^n\exp\left(-\frac{|\omega_i|}{b}\right)\), 可以得到最小二乘方法加L1正则项的结果.