0%

EM算法

发表于 更新于 分类于

前言:本文主要是关于EM算法, 这是用来求解隐变量模型的算法, 主要参考了Coursera上国立高等经济大学Advanced Machine Learning系列课程Course3: Bayesian Methods for Machine Learning Week2.

首先简单说明EM算法:

  • EM算法是一种迭代算法, 它的每次迭代由两步组成, E步, 求期望(Expectation); M步, 求极大(Maximization).
  • EM算法是一种针对隐变量模型的算法, 这里的隐变量指的是未观测到值的变量, 比方说人为引入的变量或是数据缺失的变量. 针对隐变量模型的算法有多种, EM是其中兼顾了高效以及精度的方法, 因此比较流行.
  • 记隐变量为\(T\), 数据为\(X\), 未知参数为\(\theta\), 乍看之下, EM算法是对\(\log P(X\mid\theta)\)的极大似然估计, 但其每一步迭代又给出了隐变量\(T\)的概率分布以及\(\theta\)的点估计.

隐变量模型

隐变量模型, 隐变量模型含有未观测到值的变量, 且该隐变量解释了观测到的变量之间的相关性(局部独立性), 简言之引进的隐变量不能没有用.

下面举一个隐变量模型的例子, 例子来自Week2的课件:

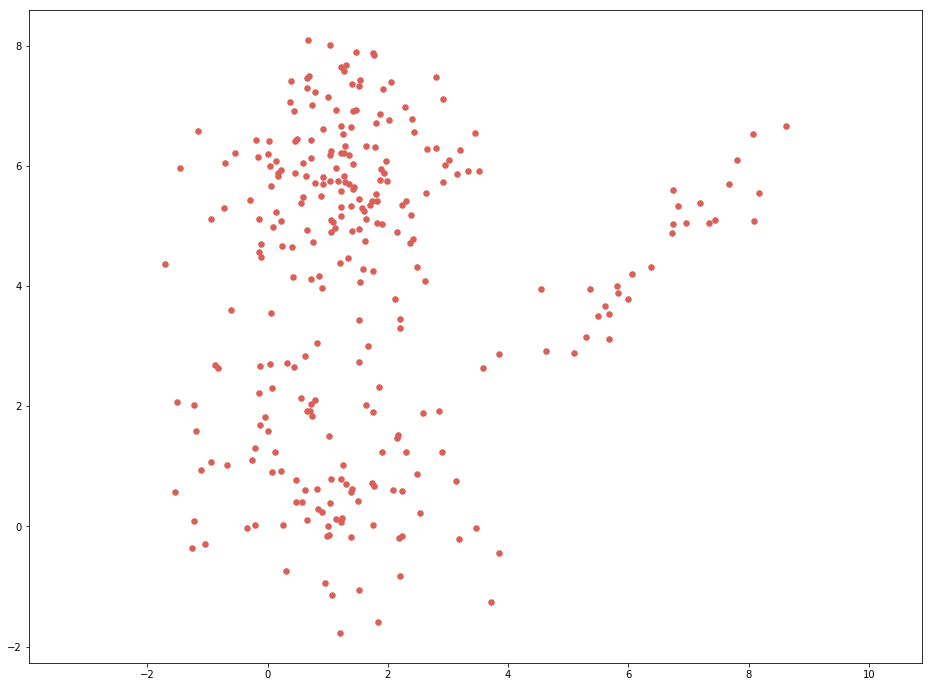
  • 考虑银行是否发放信用卡的问题, 现有客户收入及负债的数据如下图:
    通过探索性数据分析发现客户可大致分为三类, 并假定每一类服从高斯分布, 故可以采用高斯混合模型(Gaussian Mixture Model: GMM), 此时模型为:\[P(x\mid\theta)=\pi_1N(\mu_1,\Sigma_1)+\pi_2N(\mu_2,\Sigma_2)+\pi_3N(\mu_3,\Sigma_3)\]其中\(\theta=\{\pi_1, \pi_2\, \pi_3,\mu_1, \mu_2, \mu_3, \Sigma_1, \Sigma_2, \Sigma_3\}\), 且\(\pi_1+\pi_2+\pi_3=1\). 引入隐变量\(t\), \(t=1,2or3\)代表了客户所属人群类别, 显然我们没有隐变量\(t\)的观测值. 假定\[P(t=c\mid\theta)=\pi_c$, $P(x\mid t=c, \theta)=N(\mu_c, \Sigma_c)\]我们就有了:\[P(x\mid\theta)=\sum_{c=1}^3P(x\mid t=c, \theta)P(t=c\mid\theta)\]目标则是对最大化上式得到参数值\(\theta\). 故对于每一个样本\(x_i\), 计算\(P(t=c\mid x_i, \theta)\)从而推测出其所属类别.

EM算法

汇总一下上文叙述的GMM模型:\[P(x\mid\theta)=\sum_{c=1}^3P(x\mid t=c, \theta)P(t=c\mid\theta)\]其中\(\theta=\{\pi_c, \mu_c, \Sigma_c\mid c=\{1,2,3\}\}\),且\(P(x\mid t=c, \theta)=N(\mu_c, \Sigma_c)\),\(P(t=c\mid\theta)=\pi_c\ge 0\), \(\sum_{c=1}^3\pi_c=1\)如果能求出参数\(\theta\)的值, 此时模型就确定下来了, 一个自然地想法是极大化对数似然函数:\[\hat\theta=\arg\max_{\theta}{\log P(X\mid\theta)}\]EM算法没有直接对对数似然函数进行优化求解, 而是通过E步先求对目标函数下界的极大化逼近, 此时下界函数往往是凹函数, 再进行优化求解就简单很多, 下面来看:假设有\(m\)个样本, 对每个样本任取的概率分布\(q(t_i=c)\),\(i=1,...,m\) \[\begin{aligned} \log P(X\mid\theta)& = \sum_{i=1}^{m}\log P(x_i\mid\theta)\\\ & = \sum_{i=1}^{m}\log \sum_{c=1}^3P(x_i\mid t_i=c, \theta)P(t_i=c\mid\theta)\\\ & = \sum_{i=1}^{m}\log \sum_{c=1}^3q(t_i=c)\frac{P(x_i\mid t_i=c, \theta)P(t_i=c\mid\theta)}{q(t_i=c)}\\\ & \ge \sum_{i=1}^{m} \sum_{c=1}^3q(t_i=c)\log\frac{P(x_i\mid t_i=c, \theta)P(t_i=c\mid\theta)}{q(t_i=c)}\\\ & \doteq \mathcal{L}(\theta, q) \end{aligned}\] 其中唯一的一个不等号用到了Jensen不等式(概率形式), 其余等号都是基本的化简. 值得注意的是这里的\(q\)是任取的: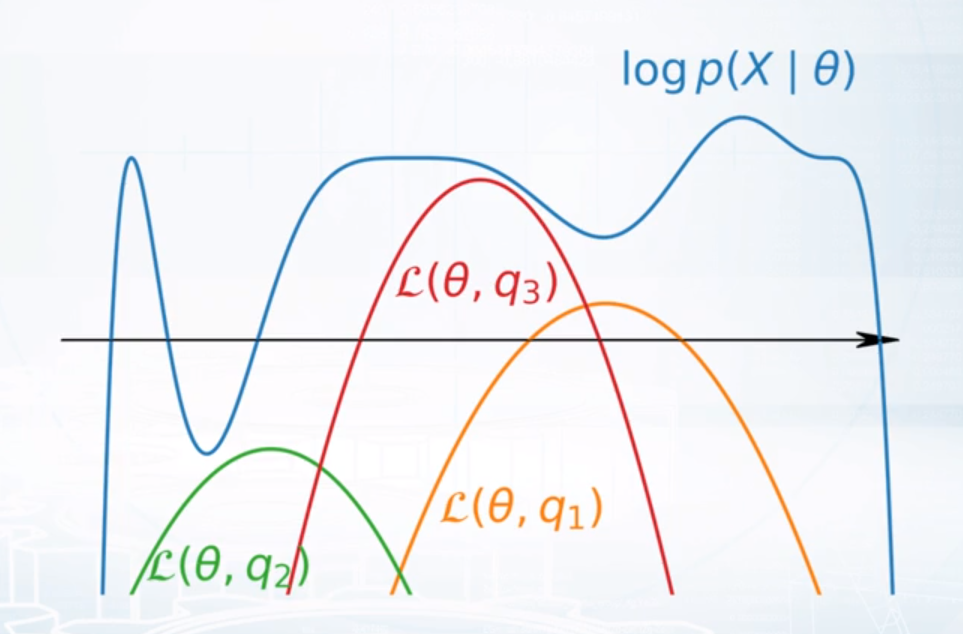

下面做的事情则是考虑在\(\theta\)给定的情况下, 如何取\(q\)才能让\(\mathcal{L}(\theta, q)\)尽可能的靠近\(\log P(X\mid\theta)\). 事实上, 观察两者之差可以发现: \[\begin{aligned} \log P(X\mid\theta)-\mathcal{L}(\theta, q)& = \sum_{i=1}^{m}\log P(x_i\mid\theta)-\sum_{i=1}^{m} \sum_{c=1}^3q(t_i=c)\log\frac{P(x_i\mid t_i=c, \theta)P(t_i=c\mid\theta)}{q(t_i=c)}\\\ & = \sum_{i=1}^{m} \sum_{c=1}^3q(t_i=c)\left(\log P(x_i\mid\theta)-\log\frac{P(x_i\mid t_i=c, \theta)P(t_i=c\mid\theta)}{q(t_i=c)}\right)\\\ & = \sum_{i=1}^{m} \sum_{c=1}^3q(t_i=c)\log\frac{P(x_i\mid\theta)q(t_i=c)}{P(x_i, t_i=c\mid \theta)}\\\ & = \sum_{i=1}^{m} \sum_{c=1}^3q(t_i=c)\log\frac{q(t_i=c)}{P(t_i=c\mid x_i, \theta)}\\\ & = \mathcal{KL}(q(T)\Vert P(T\mid X, \theta)) \end{aligned}\]恰为某\(\mathcal{KL}\)散度, \(\mathcal{KL}\)散度定义见维基百科, \(\mathcal{KL}\)散度定义为两个分布之间距离的度量, 必然\(\ge 0\), 且只在两个分布相同的情况下取\(0\). 可取\(q(T)=P(T\mid X, \theta)\). 最后对下界函数\(\mathcal{L}(\theta, q)\)稍作化简: \[\begin{aligned} \mathcal{L}(\theta, q)& = \sum_{i=1}^{m} \sum_{c=1}^3q(t_i=c)\log\frac{P(x_i\mid t_i=c, \theta)P(t_i=c\mid\theta)}{q(t_i=c)}\\\ & = \sum_{i=1}^{m} \sum_{c=1}^3q(t_i=c)\log P(x_i, t_i=c\mid \theta)-\sum_{i=1}^{m} \sum_{c=1}^3q(t_i=c)\log q(t_i=c)\\\ & = \mathbb{E}_q\log P(X, T\mid\theta)+C \end{aligned}\]这里\(C\)与\(\theta\)无关, 此时EM算法已经出来了, 第k+1次迭代, 参数为\(\theta^k\):

  1. E步求期望:求\(\mathbb{E}_{q^{k+1}}\log P(X, T\mid\theta)\), 其中\(q^{k+1}(T)=P(T\mid X, \theta^k)\)(有些书会说E步是求隐变量的分布, 但个人觉得称其为求期望的一步会比较恰当).
  2. M步求极大: \(\theta^{k+1}=\arg\max_{\theta}\mathbb{E}_{q^{k+1}}\log P(X, T\mid\theta)\).

EM算法收敛性

易得\(\log P(X\mid\theta^{k+1})\ge\mathcal{L}(\theta^{k+1}, q^{k+1})\ge\mathcal{L}(\theta^{k}, q^{k+1})=\log P(X\mid\theta^{k})\), 其中第一个不等号因为对于任意的\(q\)不等号都成立; 第二个不等号由M步易得; 第三个等号由E步易得.

GMM模型的EM算法

为了加深印象, 将

  • \(P(x\mid t=c, \theta)=N(\mu_c, \Sigma_c)\)
  • \(P(t=c\mid\theta)=\pi_c\ge 0\)
  • \(\sum_{c=1}^3\pi_c=1\)

条件带入来走一遍EM算法流程, 这里建议读者手动算一遍.第k+1次迭代, 参数为\(\theta^k\), 并计算\[P(t_i=c\mid x_i, \theta^k)=\frac{P(x_i\mid t_i=c, \theta_k)P(t_i=c\mid \theta_k)}{\sum_{c=1}^3P(x_i\mid t_i=c, \theta_k)P(t_i=c\mid \theta_k)}\]

  1. E步: 求\(\mathbb{E}_{q^{k+1}}\log P(X, T\mid\theta)\), 其中\(q^{k+1}(t_i=c)=P(t_i=c\mid x_i, \theta^k)\):\[\begin{aligned} \mathbb{E}_{q^{k+1}}\log P(X, T\mid\theta)& = \sum_{i=1}^{m} \sum_{c=1}^3P(t_i=c\mid x_i, \theta^k)\log P(x_i, t_i=c\mid \theta)\\\ & = \sum_{i=1}^{m} \sum_{c=1}^3P(t_i=c\mid x_i, \theta^k)\log P(x_i\mid t_i=c, \theta)P(t_i=c\mid\theta)\\\ & = \sum_{i=1}^{m} \sum_{c=1}^3P(t_i=c\mid x_i, \theta^k)\left(\log\frac{\pi_c}{\sqrt{(2\pi)^d|\Sigma_c|}}-\frac{1}{2}(x_i-\mu_c)^T\Sigma_c^{-1}(x_i-\mu_c)\right) \end{aligned}\]
  2. M步: 令\(\frac{\partial\mathbb{E}_{q^{k+1}}\log P(X, T\mid\theta)}{\partial \mu_c}=0\), 可得\(\sum_{i=1}^{m}P(t_i=c\mid x_i, \theta^k)(-\Sigma_c^{-1}(x_i-\mu_c))=0\),即\[\mu_c=\frac{\sum_{i=1}^{m}P(t_i=c\mid x_i, \theta^k)x_i}{\sum_{i=1}^{m}P(t_i=c\mid x_i, \theta^k)}\]对\(\Sigma_c\)求导时遇到了一些困难, 这里做出一些简化假设, 即令\(\Sigma_c=\sigma_c^2 I\), 令\(\frac{\partial\mathbb{E}_{q^{k+1}}\log P(X, T\mid\theta)}{\partial \sigma_c}=0\), 可得\[\sigma_c^2=\frac{\sum_{i=1}^{m}P(t_i=c\mid x_i, \theta^k)(x_i-\mu_c)^T(x_i-\mu_c)}{\sum_{i=1}^{m}P(t_i=c\mid x_i, \theta^k)}\]至于对\(\pi_c\)这样的有一个等式约束的优化可以用拉格朗日乘子法:\[\pi_c=\frac{\sum_{i=1}^{m}P(t_i=c\mid x_i, \theta^k)}{m}\]

GMM模型的EM算法的Python实现

首先下载数据集, 放在与py文件同一目录下.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
# -*- coding: utf-8 -*-
"""
Created on Mon Sep  3 00:19:21 2018
@author: msgsxj
"""
import numpy as np
from numpy.linalg import  solve
#!conda install -c conda-forge pyqt=4 -y
import matplotlib.pyplot as plt

samples = np.load('samples.npz')
X = samples['data']
pi0 = samples['pi0']
mu0 = samples['mu0']
sigma0 = samples['sigma0']
print(pi0)
print(mu0.shape)

plt.scatter(X[:, 0], X[:, 1], c='grey', s=30)
plt.axis('equal')
plt.show()

def E_step(X, pi, mu, sigma):
    """
    Performs E-step on GMM model
    Each input is numpy array:
    X: (N x d), data points
    pi: (C), mixture component weights
    mu: (C x d), mixture component means
    sigma: (C x d x d), mixture component covariance matrices
    Returns:
    gamma: (N x C), probabilities of clusters for objects
    """
    N = X.shape[0] # number of objects
    C = pi.shape[0] # number of clusters
    d = mu.shape[1] # dimension of each object
    gamma = np.zeros((N, C)) # distribution q(T)
    # compute det of sigma
    sigma_det = []
    for j in range(C):
        sign, logdet = np.linalg.slogdet(sigma[j])
        sigma_det.append(sign * np.exp(logdet))
    for i in range(N):
        for j in range(C):
            gamma[i, j] = np.power(sigma_det[j], -0.5) * np.exp(-0.5 * np.dot(X[i,:] - mu[j], solve(sigma[j], X[i,:] - mu[j]))) * pi[j]
        gamma[i,:] /= sum(gamma[i,:])
    return gamma

def M_step(X, gamma):
    """
    Performs M-step on GMM model
    Each input is numpy array:
    X: (N x d), data points
    gamma: (N x C), distribution q(T)
    Returns:
    pi: (C)
    mu: (C x d)
    sigma: (C x d x d)
    """
    N = X.shape[0] # number of objects
    C = gamma.shape[1] # number of clusters
    d = X.shape[1] # dimension of each object
    mu = np.zeros((C, d))
    for j in range(C):
        mu[j,:] = np.sum(np.transpose(np.multiply(gamma[:,j], np.transpose(X))), axis = 0)/np.sum(gamma[:,j])
    sigma = np.zeros((C, d, d))
    for j in range(C):
        for i in range(N):
            sigma[j,:,:] += np.multiply(gamma[i,j], np.outer(X[i,:] - mu[j,:], X[i,:] - mu[j,:]))
        sigma[j,:,:] /= np.sum(gamma[:,j])
    pi = np.zeros((C,))
    for j in range(C):
        pi[j] = np.sum(gamma[:,j])/N
    return pi, mu, sigma

def compute_vlb(X, pi, mu, sigma, gamma):
    """
    Each input is numpy array:
    X: (N x d), data points
    gamma: (N x C), distribution q(T)
    pi: (C)
    mu: (C x d)
    sigma: (C x d x d)
    Returns value of variational lower bound
    """
    N = X.shape[0] # number of objects
    C = gamma.shape[1] # number of clusters
    d = X.shape[1] # dimension of each object
    # compute det of sigma
    sigma_det = []
    for j in range(C):
        sign, logdet = np.linalg.slogdet(sigma[j])
        sigma_det.append(sign * np.exp(logdet))
    loss = 0
    for i in range(N):
        for j in range(C):
            loss += gamma[i ,j] * (np.log(pi[j]) +
                                   np.log(1/np.sqrt(np.power(2 * np.pi, d) * sigma_det[j])) -0.5 * np.dot(X[i,:] - mu[j], solve(sigma[j], X[i,:] - mu[j])) -
                                   np.log(gamma[i,j]))
    return loss

def train_EM(X, C, rtol=1e-3, max_iter=100, restarts=10):
    '''
    Starts with random initialization *restarts* times
    Runs optimization until saturation with *rtol* reached
    or *max_iter* iterations were made.
    X: (N, d), data points
    C: int, number of clusters
    '''
    N = X.shape[0] # number of objects
    d = X.shape[1] # dimension of each object
    best_loss = 0
    best_pi = np.zeros((C,))
    best_mu = np.zeros((C, d))
    best_sigma = np.zeros((C, d, d))
    for _ in range(restarts):
        try:
            temp = np.random.random(C)
            best_pi = temp/np.sum(temp)
            best_sigma[:,:,:] = np.eye(2)
            best_mu = X[np.random.randint(N, size=3),:]
            gamma = E_step(X, best_pi, best_mu, best_sigma)
            best_pi, best_mu, best_sigma = M_step(X, gamma)
            loss_pre = compute_vlb(X, best_pi, best_mu, best_sigma, gamma)
            for i in range(max_iter):
                gamma = E_step(X, best_pi, best_mu, best_sigma)
                best_pi, best_mu, best_sigma = M_step(X, gamma)
                best_loss = compute_vlb(X, best_pi, best_mu, best_sigma, gamma)
                if(np.abs((best_loss - loss_pre)/loss_pre)<rtol):
                    break
                loss_pre = best_loss
        except np.linalg.LinAlgError:
            print("Singular matrix: components collapsed")
            pass
    return best_loss, best_pi, best_mu, best_sigma

best_loss, best_pi, best_mu, best_sigma = train_EM(X, 3)

gamma = E_step(X, best_pi, best_mu, best_sigma)
labels = gamma.argmax(1)
plt.figure()
plt.figure(figsize=(16, 12))
plt.scatter(X[:, 0], X[:, 1], c=labels, s=30)
plt.axis('equal')
plt.savefig("GMM_EM.png")
plt.show()
运行结果图如下:

EM算法的变体

事实上,EM算法的E步其实是采用了变分推断的方法, 变分推断又称变分贝叶斯方法, 它是用来计算难以计算积分的一类方法(求期望本质上是求积分):

  • 在一个给定分布族\(Q\)中找到\(q(T)\), 使其逼近\(P(T\mid X, \theta)\), 且一般选用最小化\(\mathcal{KL}\)散度\(\mathcal{KL}(q(T)\Vert P(T\mid X, \theta))\)
  • 计算目标积分时进行近似计算: \(\mathbb{E}_{P(T\mid X, \theta)}\log P(X,T\mid\theta)\approx \mathbb{E}_{q(T)}\log P(X,T\mid\theta)\)
  • 完整版的EM算法则可以视为此时分布族\(Q\)取得足够大了, 因而包含\(P(T\mid X, \theta)\), 也就必然有\(q(T) = P(T\mid X, \theta)\); 而一般分布族\(Q\)选取可为正态分布, 且其协方差阵为对角阵这样的简单分布.
  • 此外对变量之间做出额外的独立性假定的方法被称为是平均场近似法, 显然这样的假定能降低计算量, 这种方法、变分推断与EM算法结合可以产生不同的变体, 详见我的另外一篇博文变分贝叶斯方法.

除了变分推断, 还有三类非常著名的方法同样能够用来计算难以计算的积分, 分别是: MCMC, 期望传播(Expectation Propagation: EP)及拉普拉斯近似方法(Laplace Approximation):

  • MCMC是一类对分布进行抽样的方法: \(T_s \sim P(T\mid X, \theta)\), 其本质是构建稳态分布恰为所需分布\(P(T\mid X, \theta)\)的马尔可夫链. 概率论中的极限理论告诉我们, \(\frac{1}{M} \sum_{s=1}^M\log P(X,T_s\mid\Theta)\)会慢慢逼近\(\mathbb{E}_{P(T\mid X, \theta)}\log P(X,T\mid\Theta)\), 因此随着抽样数的增大, 其近似值会越来越精确. 这块内容详见我的另一篇博文MCMC.
  • 期望传播方法可以简单理解为变分贝叶斯中最小化的\(\mathcal{KL}\)散度逆过来, 即最小化\(\mathcal{KL}(P(T\mid X, \theta)\Vert q(T))\), 见期望传播.
  • 拉普拉斯近似方法本质上是将被积函数视为正态分布, 见拉普拉斯方法.