前言: 读PRML一书的6.4节, 对图6.4中高斯过程的采用不同核函数模拟实现非常好奇, 同时也惊叹于高斯过程看上是几乎处处连续的性质, 于是尝试用R去模拟高斯过程.
首先简单说明几点:
- 经典的随机过程(stochastic process)的定义\(\{x_t, t\in T\}\)可以简单理解为随机变量加上一个维度(比方说时间), 一般的, 时间视为不可数; 另外随机变量可以取实值, 复值, 向量值等, 但一般还是取实值.
- 由随机变量的概率空间及状态空间出发去定义随机过程概率空间却不是那么方便, 这当中用到了Kolmogorov定理, 详见钱敏平的随机过程论1.1及1.2小节.
- 另外一个重要定理可分修正表明, 任意随机过程都能修正为一个具有可分性的过程(即两者几乎处处相等), 而可分的随机过程其实带有一些连续性的味道, 可见钱敏平的随机过程论p11.
- 高斯过程则是任意有限维时间的联合分布(\(\{x_{t_1}, x_{t_2},...,x_{t_k}\}\), 其中\(t_1,..,t_k, k\)均任取)为多元正态分布的随机过程, 可见维基百科.
- 补充一点, 随机场(random field)则是可以视为随机过程的一般化, 即此时添加的可能不仅仅是一维的时间, 而是多维向量; 而高斯随机场(Gaussian random field)则是有限维联合分布为多元正态分布的随机场.
- 在现代数学中, 随机过程这个概念等同于随机场(参见随机场的维基百科).
容易知道, 多元正态分布仅仅依赖于它的期望\(\mu\)与协方差矩阵\(\Sigma\), 因此如果我们能对任意有限维分布给出期望\(\mu\)与协方差矩阵\(\Sigma\), 高斯过程也就给定了.
一种思路是假定\(\mu=0\), \(\Sigma=K\), 其中\(K_{ij}=k(t_i, t_j)\), 下面给出\(k(t_i, t_j)\)的三种形式:
- \(k(t_i, t_j)=\min\{t_i, t_j\}\), 此时高斯过程即为维纳过程, 或者说布朗运动, 高斯过程的R模拟图像如下:
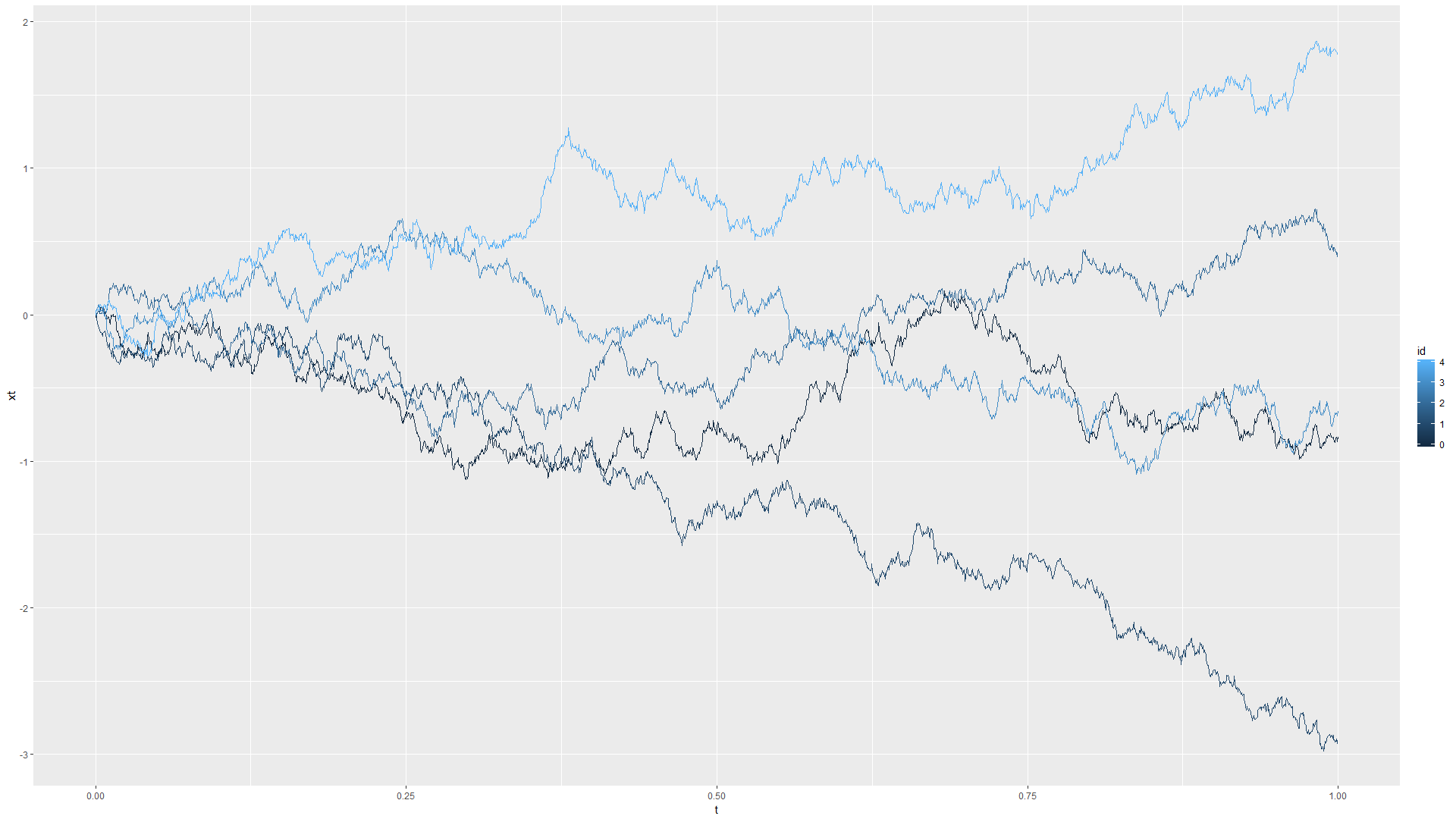
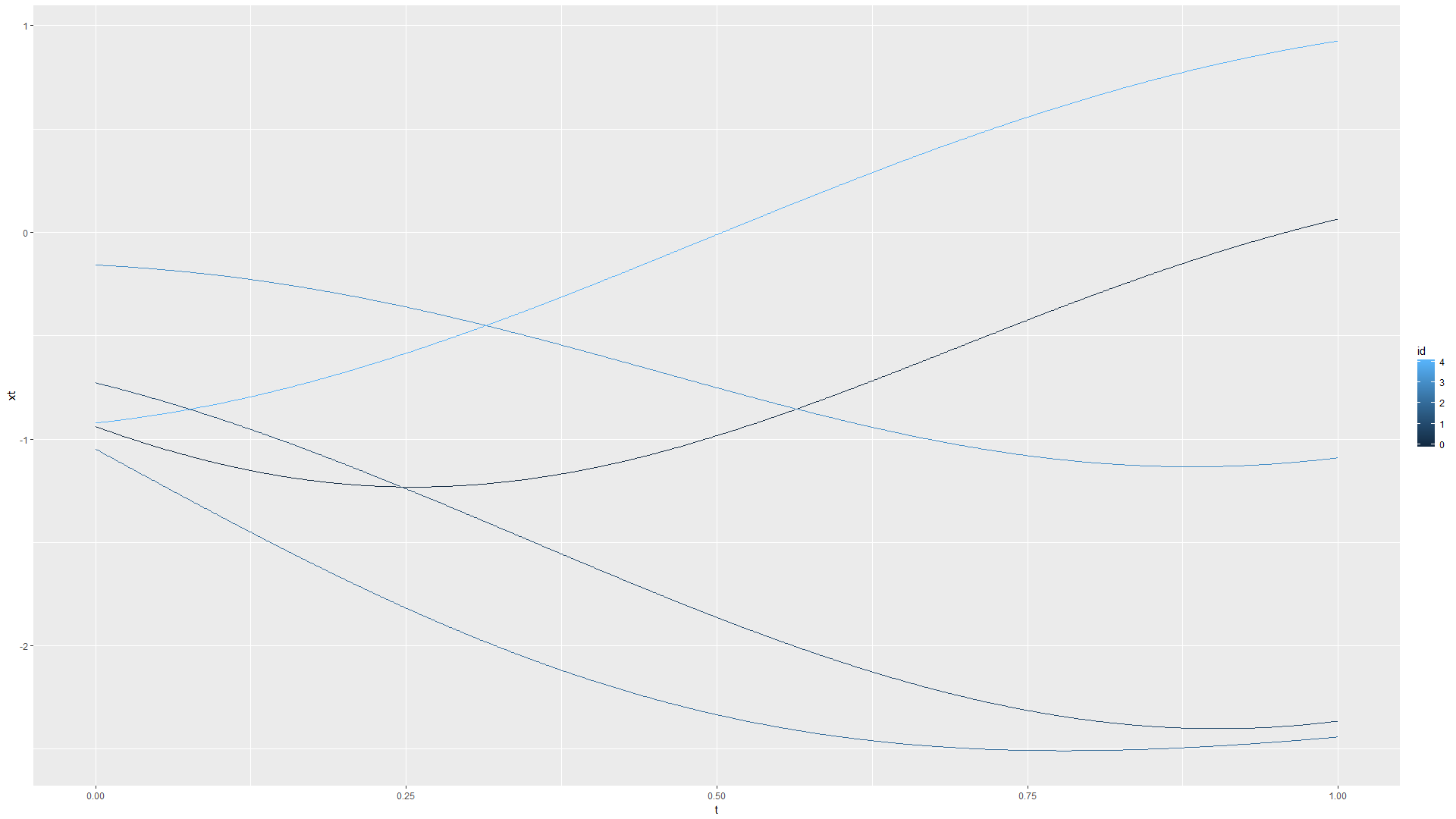
- \(k(t_i, t_j)=\exp(-\Vert t_i-t_j\Vert/2\sigma^2)\), 这个函数又被称为高斯核, 取\(2\sigma^2=1\), 高斯过程的R模拟图像如下:
取\(2\sigma^2=1/16\), 高斯过程的R模拟图像又如下:
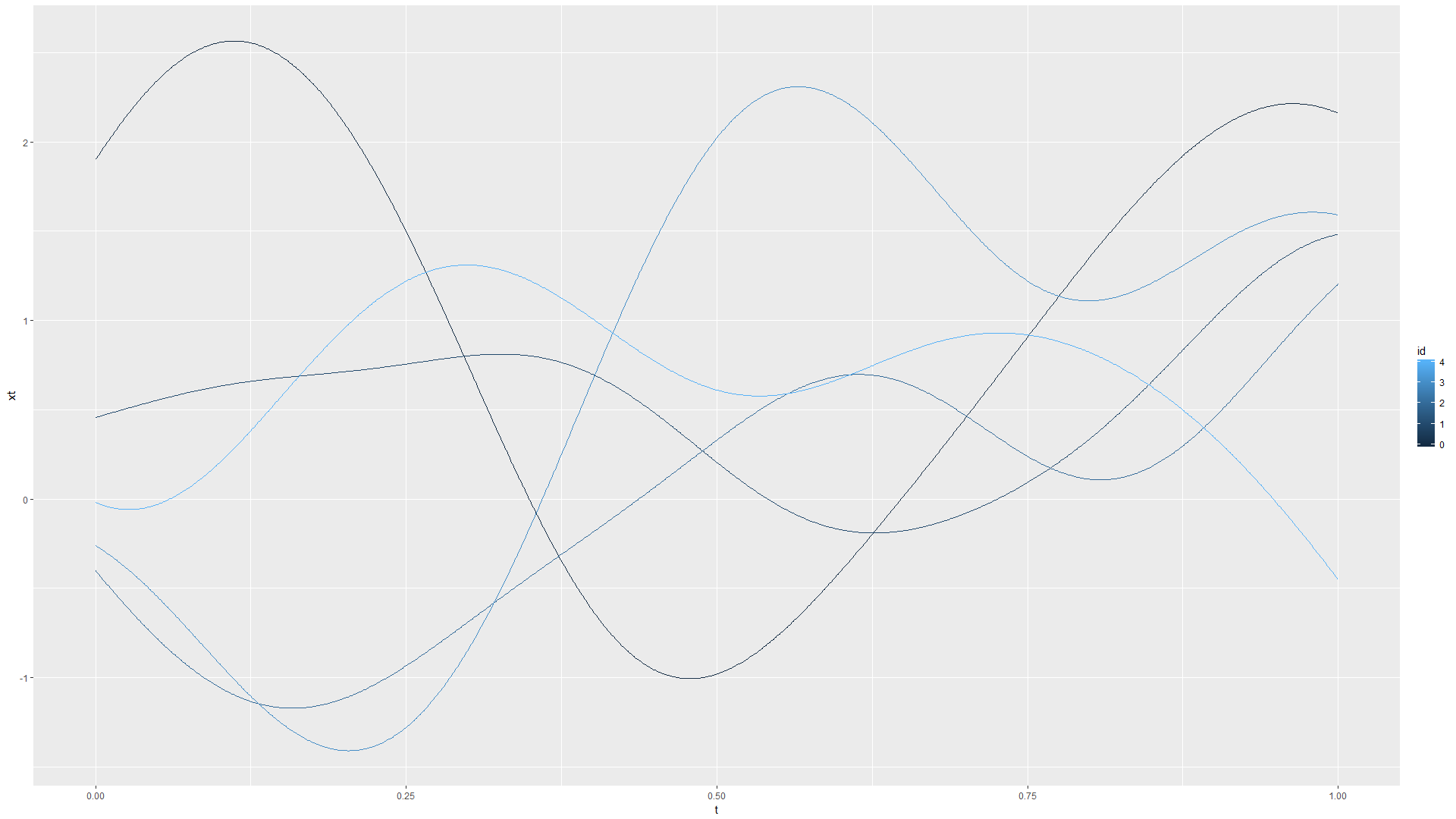
- \(k(t_i, t_j)=\exp(-\theta\Vert t_i-t_j\Vert)\), 此时高斯过程即为Ornstein–Uhlenbeck过程, 取\(\theta=1\), 高斯过程的R模拟图像如下:
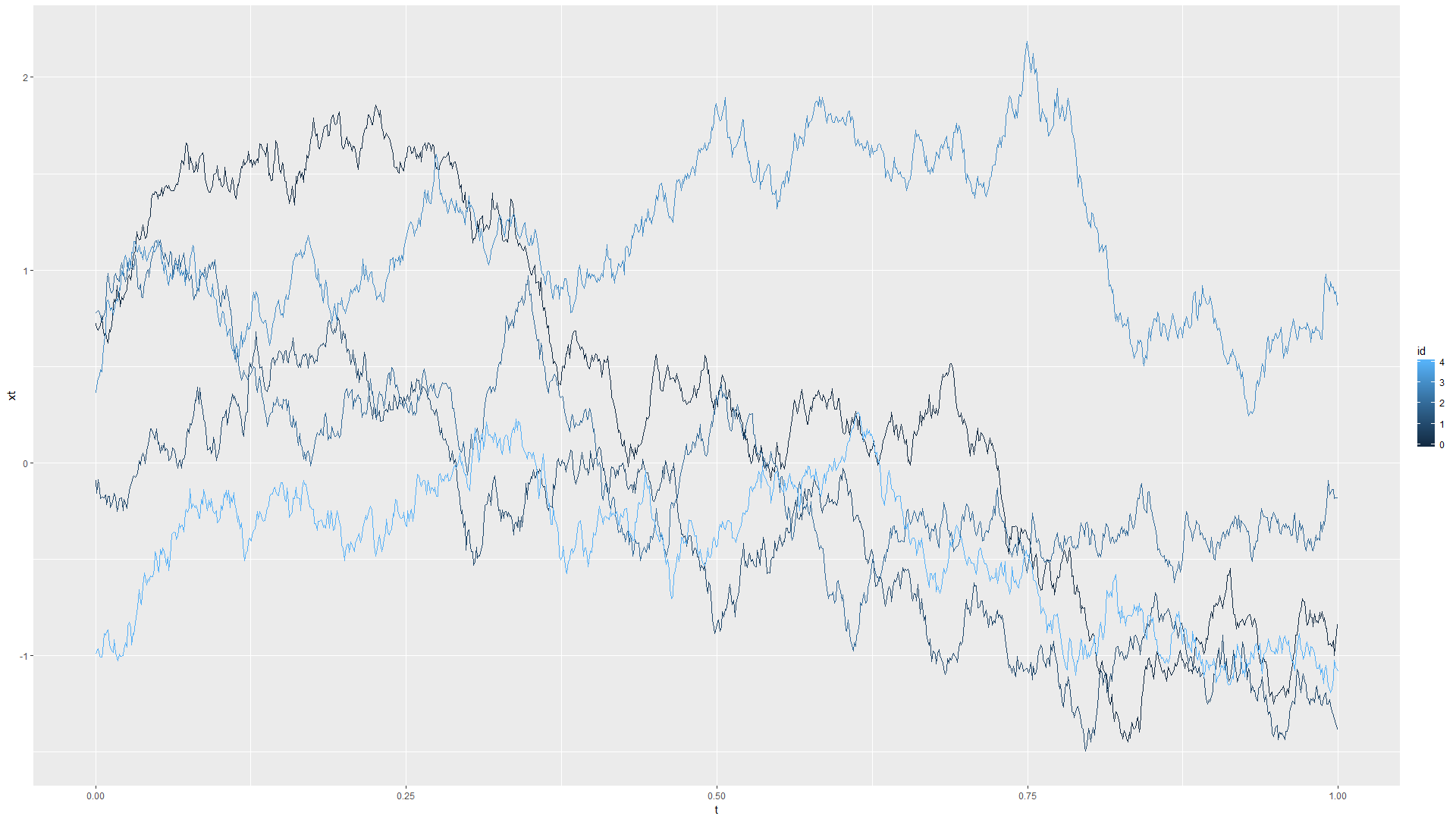
最后附上R代码, 其中核心部分代码即gaussprocess函数, 这个函数即先根据函数\(k(,)\)去求对所有时间的协方差矩阵\(\Sigma\)(计算机的计算必须离散化, 这里的模拟精度为\(t\in [0,1]\)之间有1000个数), 再用MASS包中的mvrnorm函数去从多元正态分布中抽样: 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65library(ggplot2)
library(magrittr)
library(tidyverse)
gaussprocess <- function(from = 0,
to = 1,
K = function(s, t) {min(s, t)},
start = NULL,
m = 2000) {
t <- seq(from = from, to = to, length.out = m)
Sigma <- sapply(t, function(s1) {
sapply(t, function(s2) {
K(s1, s2)
})
})
path <- MASS::mvrnorm(mu = rep(0, times = m), Sigma = Sigma)
if (!is.null(start)) {
path <- path - path[1] + start # Must always start at "start"
}
return(data.frame("t" = t, "xt" = path))
}
## 维纳过程
plot_1 <- function(times = 5) {
data <- gaussprocess()
data['id'] = 0
for(i in 1:(times-1)){
temp <- gaussprocess()
temp['id'] = i
data <- rbind(data, temp)
}
data['id']
ggplot(data = data, aes(x = t, y = xt, color = id, group = id)) + geom_line()
}
plot_1(times = 5)
## 高斯过程
plot_2 <- function(times = 5) {
data <- gaussprocess(K = function(s, t) {exp(-16 * (s - t) ^ 2)})
data['id'] = 0
for(i in 1:(times-1)){
temp <- gaussprocess(K = function(s, t) {exp(-16 * (s - t) ^ 2)})
temp['id'] = i
data <- rbind(data, temp)
}
data['id']
ggplot(data = data, aes(x = t, y = xt, color = id, group = id)) + geom_line()
}
plot_2(times = 5)
## Ornstein-Uhlenbeck过程
plot_3 <- function(times = 5) {
data <- gaussprocess(K = function(s, t){exp(-abs(s - t))})
data['id'] = 0
for(i in 1:(times-1)){
temp <- gaussprocess(K = function(s, t){exp(-abs(s - t))})
temp['id'] = i
data <- rbind(data, temp)
}
data['id']
ggplot(data = data, aes(x = t, y = xt, color = id, group = id)) + geom_line()
}
plot_3(times = 5)