Latent Dirichlet Allocation

前言: 本文主要是关于Latent Dirichlet Allocation模型, 这是一类能够从文档集合中挖掘出抽象主题的模型, 主要参考了Coursera上国立高等经济大学Advanced Machine Learning系列课程Course3: Bayesian Methods for Machine Learning Week3.

隐狄利克雷分配模型

以推荐系统为例, 假如我读过东野圭吾的新参者, 我希望推荐系统能把白夜行也推荐给我. 在自然语言处理(Natural Language Processing: NLP)中, 主题模型(Topic Model)是一类能够从文档集合中挖掘出抽象主题的模型, 其中用的最多的大概就是隐狄利克雷分配模型(Latent Dirichlet Allocation: LDA). 比方说给定50个主题数量, 其想法是对每一篇文档给出一个关于50个主题数量的分布, 例如新参者的主题是70%的推理类, 10%的叉叉类等, 因此如果能得到每篇文档的主题分布, 就能给出书之间的相似度.

下面我们来看什么是LDA模型, 并给出一些记号. 假设有文档$D$篇, 其中第$d$篇文档有$N_d$个单词, 给定主题数量$T$, 记第$d$篇文档的主题为$\theta_d$, 显然$\theta_d$为一个$T$维向量, $z_{dn}$是第$d$篇文档的第$n$个单词的主题分布, $w_{dn}$是第$d$篇文档的第$n$个单词本身(一般给长度为$\left|w_{set}\right|$定词汇表$w_{set}$后用一个长度为$\left|w_{set}\right|$的向量去表示).

给定主题数量$T=50$, 目前我们有了三个关键要素:

每篇文档的主题分布:$\theta$
每篇文档每个单词的主题分布:$z$
每篇文档每个单词:$w$

遵循一些直观的假象, 我们分三步尝试去构造模型:

首先要有每篇文档的主题$\theta_d$, 其中$d\in\{1,2,...,D\}$.
简单假设每个单词的主题$z_{dn}$与所在文档的主题$\theta_d$一致, 其中$n\in\{1,2,...,N_d\}$.
每个单词确定了主题之后就能按照一定的概率分布从主题中选择单词出来. 比方说给定词汇表$w_{set}$, 其包含$\left|w_{set}\right|$个单词, 假设第$t$主题有一个单词表上的概率分布$\varphi_{\cdot t}$, 显然$\varphi_{\cdot t}$为$\left|w_{set}\right|$维列向量, 那么$\varphi$为$\left|w_{set}\right|\times T$的未知参数矩阵.

将上述三要素视为随机变量, 此时可以写出三者的联合分布函数: \[P(W, Z, \Theta)=\prod_{d=1}^{D}P(\theta_d)\prod_{n=1}^{N_d}P(z_{dn}\mid\theta_d)P(w_{dn}\mid z_{dn})\]显然文档主题$\theta_d$和单词主题$z_{dn}$是无法观测得到的, 因此作为LDA模型中的L(Lantent), D(Dirichlet)则是指随机变量$\theta_d$满足Dirichlet分布:

假定文章的来源一致, 即$\theta_d$独立同分布: 服从Dirichlet分布$\theta_d\sim Dir(\alpha)=\frac{1}{B(\alpha)}\prod_{t=1}^{T}\theta_{dt}^{\alpha_t-1}$, 其中$\alpha$为$T$维列向量; $B(\alpha)$为多元Beta函数, 可表示为$B(\alpha)=\frac{\prod_{i=1}^{T}\Gamma(\alpha_i)}{\Gamma(\sum_{i=1}^{T}\alpha_i)}$, $\Gamma$为Gamma函数, 详见维基百科.
值得注意的是, $\alpha$增大能导致每篇文档的话题数量变多(关于这点可以参考维基百科上的一张动图), 所以另一种思路是把$\alpha$视为超参去调.
假定每个单词的主题$z_{dn}$与所在文档的主题$\theta_d$一致, 即$P(z_{dn}\mid\theta_d)=\theta_{dz_{dn}}$, 写得直观些, 即$P(z_{dn}=t\mid\theta_d)=\theta_{dt}$, $\theta_{dt}$表示$\theta_d$的第$t$个分量.
$T$个主题与词汇表$w_{set}$的分布记为$\phi$, 这里的$\phi$为$\left|w_{set}\right|\times T$的矩阵. 即$P(w_{dn}\mid z_{dn})=\varphi_{z_{dn}w_{dn}}$, 写得直观些, $v$为不超过$\left|w_{set}\right|$的正整数, $P(w_{dn}=v\mid z_{dn})=\varphi_{v z_{dn}}$.

若用大小字母表示小写字母的总和, 参数仍简记为小写字母, 我们现有五个关键要素: $W$为数据集; $Z, \Theta$为隐变量; $\varphi, \alpha$为未知参数.

板表示法(plate notation)是一种表示在图形模型中重复的变量的方法, 下面采用板表示法的贝叶斯网络表达上述模型: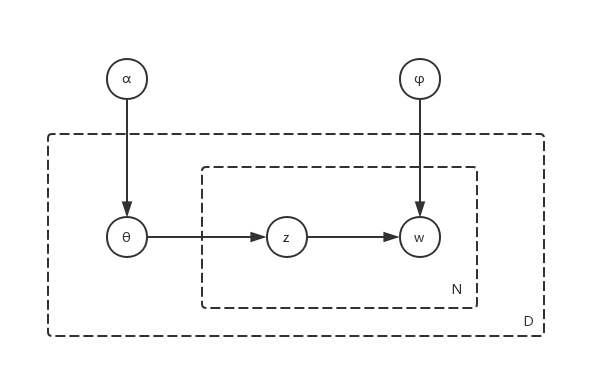

这里的虚线框右下角的字母表示框中的部分应该重复画字母次, 所以板表示法的好处就很明显:

简化图模型,更美观.
同时模型表达式变得一模了然.

最后把该LDA模型用较为简练的语言再写一遍(可以对照图去写): \[P(W, Z, \Theta\mid \varphi, \alpha)=\prod_{d=1}^{D}P(\theta_d)\prod_{n=1}^{N_d}P(z_{dn}\mid\theta_d)P(w_{dn}\mid z_{dn})\]其中:

$\theta_d\sim Dir(\alpha)=\frac{1}{B(\alpha)}\prod_{t=1}^{T}\theta_{dt}^{\alpha_t-1}$, 其中$d\in\{1,2,...,D\}$, $T$给定.
$P(z_{dn}\mid\theta_d)=\theta_{dz_{dn}}$, 其中$n\in\{1,2,...,N_d\}$.
$P(w_{dn}\mid z_{dn})=\varphi_{w_{dn}z_{dn}}$, 给定词汇表$w_{set}$, $w_{dn}\in\{1,2,...,\left|w_{set}\right|\}$.

大小字母表示小写字母的总和, 参数仍简记为小写字母, 总结如下:

未知:$Z, \Theta$为隐变量; $\varphi, \alpha$未知参数.
已知:$W$为数据集, $D$为文档数量, $N_d$为每篇文档单词数.
超参:主题数$T$, 词汇表$w_{set}$(可以取为这些文档出现过的单词组成的集合).

这个模型因为属于隐变量模型, 故可用EM算法求解: 第k+1次迭代, 当前参数为$\varphi^k, \alpha^k$:

E步求期望:求$\mathbb{E}_{q^{k+1}}\log P(W, Z, \Theta\mid\varphi, \alpha)$, 其中$q^{k+1}(Z, \Theta)=P(Z, \Theta\mid W, \varphi^k, \alpha^k)$.
M步求max: $(\varphi^{k+1}, \alpha^{k+1})=\arg\max_{(\varphi, \alpha)}\mathbb{E}_{q^{k+1}}\log P(W, Z, \Theta\mid\varphi, \alpha)$.

若后验$P(Z, \Theta\mid W, \varphi^k, \alpha^k)$难以处理, 则可以用一些近似方法取求得期望, 如变分贝叶斯, Laplace近似方法, 期望传播方法, MCMC方法等

LDA模型的拓展

$\Phi$

若把未知参数$\varphi$视为随机变量, 重新记为$\Phi$, 假定$\Phi_{i\cdot}\sim Dir(\beta_i)$, 即假定第$i$个单词的主题分布满足参数为$\beta_i$的狄利克雷分布(回忆开头狄利克雷分布的特性), 这里假定$i$的取值集合$w_{set}$的大小为$S$, 上述修改后的模型用板表示法表示如下: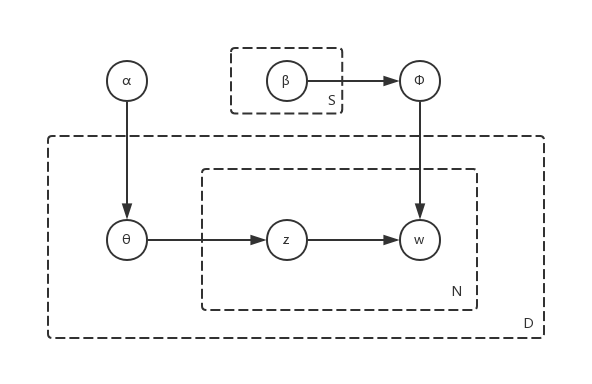

\[P(W, Z, \Theta, \Phi\mid \alpha, \beta)=\prod_{d=1}^{D}P(\theta_d)\prod_{n=1}^{N_d}\prod_{i=1}^{S}P(z_{dn}=i\mid\theta_d)P(w_{dn}\mid z_{dn}=i, \Phi_{i\cdot})P(\Phi_{i\cdot})\]与上文的模型相比只是把参数$\varphi$视为随机变量$\Phi$, 且$\Phi_{i\cdot}\sim Dir(\beta_i)$, 其余不变. 总结如下:

未知:$Z, \Theta, \Phi$为隐变量; $ , $为未知参数.
已知:$W$为数据集, $D$为文档数量, $N_d$为每篇文档单词数.
超参:主题数$T$, 词汇表$w_{set}$(可以取为这些文档出现过的单词组成的集合).

Logit-normal distribution

$\theta_d\sim Dir(\alpha)$的一个良好替代是假定$\theta_d\sim \mathcal{P}(N(\mu, \Sigma))$, 即满足Logit-normal分布. 逻辑正态分布: 若$Y\sim N(\mu, \Sigma)$, 则称$X=\mathcal{P}(Y)$为逻辑正态(Logit-normal)分布, 其中$\mathcal{P}()$为逻辑函数. 下面来看这两个分布的异同:

与狄利克雷分布相比, 逻辑正态分布能捕捉$\theta_d$之间的相关性, 因而更受欢迎.
虽然任何参数$\mu, \Sigma, \alpha$的选择都不能让两个的密度函数相等, 但通过最小化$\mathcal{KL}$散度的方式来让逻辑正态分布去逼近狄利克雷分布的方式, 即最小化\[\mathcal{KL}(p, q)=\int p(x\mid \alpha)\log\frac{p(x\mid\alpha)}{q(x\mid\mu, \Sigma)}dx\]可以得到关于$\alpha$的参数$\mu,\Sigma$在$\mathcal{KL}$散度意义下的最优选择, 详见维基百科, 这里要说明的是, 当$\alpha$的每个分量都趋于无穷, $p(x\mid \alpha)\to q(x\mid\mu, \Sigma)$, 也就是说$\alpha$很大时两者可以变得非常靠近.

Dynamic Topic Models

此外还有动态主题模型, 见这篇文章

隐狄利克雷分配模型

LDA模型的拓展

\(\Phi\)

Logit-normal distribution

Dynamic Topic Models