前言: 本文的初衷是试图用尽量简明形象的语言说一说scipy.optimize.minimize函数涉及到的经典优化算法的特点, 方便速查与快速回忆; 严格理论的部分可见官方文档Notes部分的内容, 其对每一种方法都给出了参考论文, 而笔者关于这些算法的理解大多来自于Jorge Nocedal的Numerical Optimization.
首先来看scipy.optimize这个包的官方文档, 右侧的目录告诉我们这个包大致分为6块内容:
- 多元函数无约束优化
- 多元函数约束优化
- 最小二乘优化
- 一元函数优化
- 自定义优化器
- 寻根问题
minimize函数
可以看到scipy.optimize.minimize函数对应于第一第二块内容, 具体minimize的文档, 可以看到method参数中罗列着以下14种方法:
- Nelder-Mead
- Powell
- CG
- BFGS
- Newton-CG
- L-BFGS-B
- TNC
- COBYLA
- SLSQP
- trust-constr
- dogleg
- trust-ncg
- trust-exact
- trust-krylov
优化是对目标函数的进行迭代求最小值的过程, 若优化过程只需求得目标函数的在迭代点处函数值, 那么这类方法称为是无导数优化; 若需要求得目标函数的一阶信息(梯度向量值), 那么这类方法称为是一阶方法; 若需要求得二阶信息(Hessian阵), 那么这类方法称为是二阶方法. 显然三类方法的计算量的越来越大.
上面罗列的算法中无导数优化方法有: Nelder-Mead, Powell, COBYLA; 一阶方法有: CG, BFGS, L-BFGS-B, TNC, SLSQP; 二阶方法有: Newton-CG, trust-constr, dogleg, trust-ncg, trust-exact, trust-krylov; 特别的, 二阶方法中的trust-constr, trust-ncg, trust-krylov若能提供Hessian右乘任意向量p的结果(即关于迭代点x和任意向量p的函数), 这样的函数一般来说计算量会小于直接计算Hessian阵, 因此实际上计算量会介于一阶方法与二阶方法之间, 这里笔者称之为一阶半方法, 这类方法适合大规模问题.
下面按优化问题的不同分无约束优化, 有界约束优化与约束优化分别来看:
无约束优化
Nelder-Mead方法
Nelder-Mead方法是无导数优化方法, 其保持了对\(\mathbb{R}^n\)中的\(n+1\)个点的函数值追踪, 且这些点的凸包构成了一个非退化的单纯形. 比方说目标函数为\(\mathbb{R}^2\)中的函数, Nelder-Mead方法就保持了对\(3\)个点的函数值追踪, 非退化指的是这三者不能共线.
下面以维基百科上的关于Rosenbrock函数的动图为例, 记手中的\(n+1\)个点为\(\{x_1,...,x_{n+1}\}\), 并将它们按函数值大小排序\(f(x_1)\le\cdots\le f(x_{n+1})\), \(n\)个最好的点的形心为\(\bar{x}=\frac{1}{n}\sum_{i=1}^n x_i\)此时\(\bar{x}\)与最差的点\(x_{n+1}\)之间的连线即为: \[\bar{x}(t)=\bar{x}+t(x_{n+1}-\bar{x})\]Nelder-Mead方法出于尽量远离函数值最高的点的想法, 去观察\(\bar{x}(-1)\)的值
- 若\(f(x_1)\le f(\bar{x}(-1))<f(x_n)\), 则用\(\bar{x}(-1)\)取代\(x_{n+1}\);
- 若\(f(\bar{x}(-1))<f(x_1)\), 继续观察\(\bar{x}(-2)\)是否会带来更进一步下降, 择优选择取代\(x_{n+1}\);
- 若\(f(x_n)\le f(\bar{x}(-1))<f(x_{n+1})\), 先后观察\(\bar{x}(-\frac{1}{2})\)与\(\bar{x}(\frac{1}{2})\)是否会带来更进一步下降, 注意到先后的顺序也体现了尽量远离\(x_{n+1}\);
- 最后若上述条件均不满足, 则整体向函数值最小的点\(x_1\)挪一半.

Powell方法
Powell方法是共轭方向法的一种变体, 先来看什么是共轭方向法, 共轭方向法是给定一共轭方向的集合\(\{p_1....,p_n\}\), 对集合中的方向依次进一维巡查的方法, 因此显然是无导数优化方法.
以最简单的二次函数\(f(x)=\frac{1}{2}x^TAx-b^Tx\)为例, 其中\(A\)为\(n\)阶对称正定方阵, 此时共轭的概念有了具体的要求: \(p_i^TAp_j=0\). 若\(A\)恰为对角阵, 如左图所示, 共轭方向集合可取为坐标轴方向\(\{e_1, e_2\}\); 若\(A\)不为对角阵, 如右图所示, 此时\(\{e_1, e_2\}\)不能作为一组共轭方向, 图中的红线和蓝线则是给出了两个不同的共轭方向集合.
值得注意的是, 此时至多\(n\)步共轭方向法会收敛到最小值点\(x^*\), 证明可见Numerical Optimization一书定理5.1
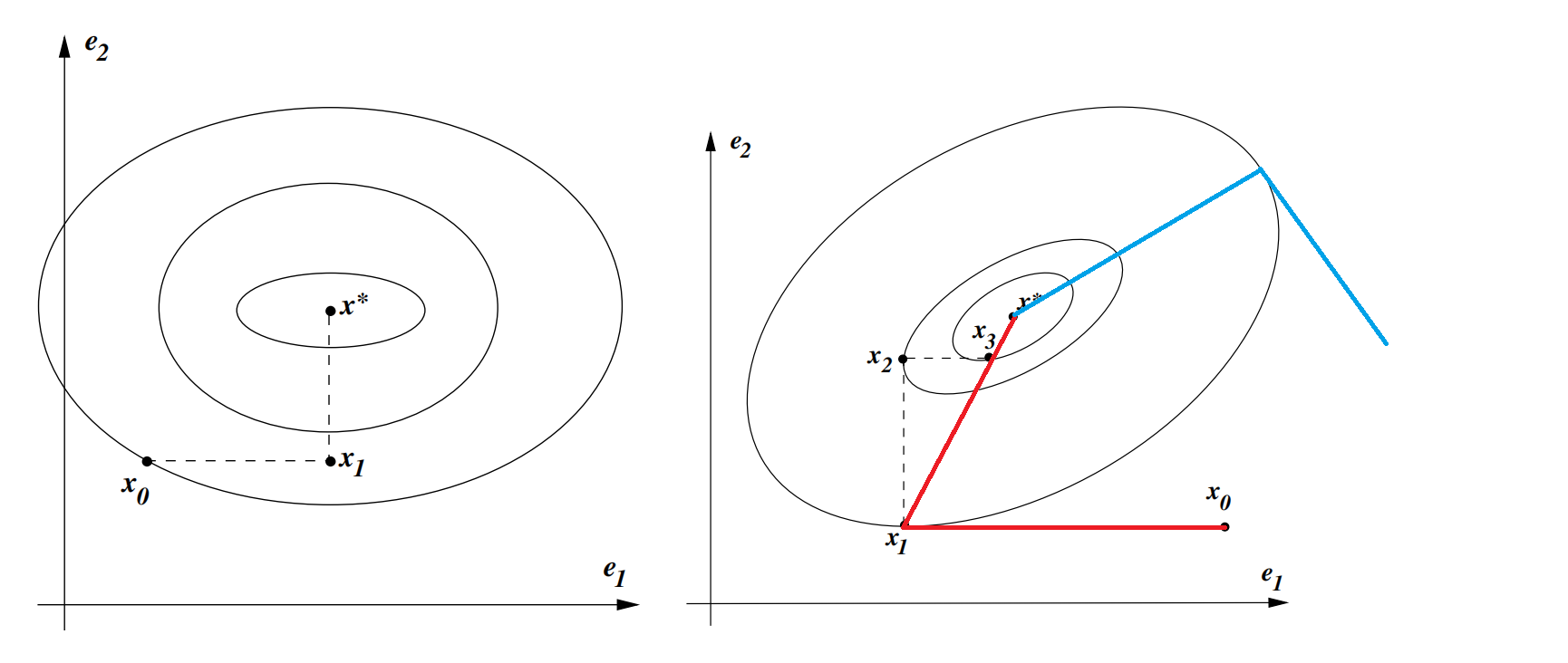
回到Powell方法, 仍然以上述二次函数为例, 其与标准共轭方向法唯一的不同在于迭代地得到共轭方向的集合, 且共轭方向的集合的初始化可简单取为\(\{e_1, e_2\}\). 以右图为例,
- 第一步从\(x_0\)出发沿着\(e_1\)做一维巡查得到\(x_1\);
- 第二步先分别对\(\{e_2,e_1\}\)做一维巡查得到\(x_2,x_3\), 由此得到真巡查方向\(x_3-x_1\), 从\(x_1\)出发沿着\(x_3-x_1\)做一维巡查就能直接到达\(x^*\)(不难验证\(x_3-x_1\)与\(e_1\)关于\(A\)共轭), 且此时共轭方向的集合更新为\(\{e_1, x_3-x_1\}\).
容易看到Powell方法不涉及一阶信息因此为无导数优化方法. 上述括号内的性质称为是并行子空间性质: 记函数\(f(x)\)在两条平行线\(l_1(\alpha)=x_0+\alpha e_1\), \(l_2(\alpha)=x_2+\alpha e_1\)上的最小值点分别为\(x_1, x_3\), 那么\(x_3-x_1\)与\(e_1\)关于\(A\)共轭. 该性质也容易推广到\(n\)维情形.
上述性质可参考Numerical Optimization一书9.4节, 最后要注意的是对于一般的函数只需将精确的一维巡查改为非精确搜索.
CG方法
CG为Conjugate Gradient的缩写, 即共轭梯度法, 这是利用一组共轭方向求解线性方程组\(Ax=b\)的算法, 其中\(A\)为\(n\)阶对称正定方阵, 而共轭方向一般通过构造一个关于\(A\)的Krylov子空间来得到, 且为一阶半方法, 详见Numerical Optimization一书算法5.1. 不难发现线性方程组的求解等价于最小化二次函数\(f(x)=\frac{1}{2}x^TAx-b^Tx\). 事实上, CG方法也可用于一般的优化问题, 其与上述Powell方法类似, 共轭方向由迭代更新得到, 唯一的不同在于CG方法用了一阶甚至是二阶信息来更新共轭方向(补充一句, 对于一般的非二次函数并没有共轭一说, 这里可以理解为沿用共轭一词). 以FR(Fletcher-Reeves)方法为例: \[\beta_{k+1}^{FR}=\nabla f_{k+1}^T\nabla f_{k+1}/\nabla f_{k}^T\nabla f_{k}, p_{k+1}=-\nabla f_{k+1}+\beta_{k+1}^{FR}p_k\]其有许多变体, 具体到SciPy中的这里CG方法指的是PR(Polak-Ribiere)方法:\[\beta_{k+1}^{PR}=\nabla f_{k+1}^T(\nabla f_{k+1}-\nabla f_{k})/\nabla f_{k}^T\nabla f_{k}, p_{k+1}=-\nabla f_{k+1}+\beta_{k+1}^{FR}p_k\]此外还有PR+方法, HS方法, FR-PR方法等可见Numerical Optimization一书5.2节. 且这里除了HS方法是二阶方法, 其余涉及的均为一阶方法.
上述初值\(p_0\)可直接取为负梯度方向, 另外值得注意的是, 这里关于\(p_k\)的一维巡查方法一般需要满足强Wolfe条件, 且\(c_2<\frac{1}{2}\).
BFGS方法
BFGS作为一种的拟牛顿方法, 其不直接计算Hessian阵, 而是用梯度信息近似计算Hessian阵的逆并迭代更新, 因此是一阶方法, 其更新公式如下:\[H_{k+1}=(I-\rho_ks_ky_k^T)H_k(I-\rho_ky_ks_k^T)+\rho_ks_ks_k^T\]其中\(s_k=x_{k+1}-x_k, y_k=\nabla f_{k+1}-\nabla f_k, \rho_k=1/y_k^Ts_k>0\). 由于\(H_{k+1}\)直接为Hessian阵的逆的近似, 因此搜索方向为\(p_{k+1}=-H_{k+1}\nabla f_{k+1}\).
DFP方法与BFGS方法唯一的不同在于迭代更新Hessian阵本身而不是逆, 但由于仍然需要求逆操作, 因此计算量会比BFGS大上一圈. DFP方法的迭代公式可参考Numerical Optimization一书6.1节, 另一种的常见拟牛顿方法SR1可参考Numerical Optimization一书6.2节.
最后值得注意的是, BFGS常用Wolfe条件做为巡查条件.
Newton-CG方法
Newton-CG方法是一种截断牛顿方法, 而截断牛顿方法则是近似去解牛顿方程来得到巡查方向的思路, 解牛顿方程即为了获得牛顿方向, 而截断意味着近似解方程要在截断的迭代次数内, 因而是近似.
选用CG方法来近似求解牛顿方程(\(\nabla^2f_k p_k+\nabla f_k=0\)), 我们就得到了Newton-CG方法, 由于要求得到\(\nabla^2 f_k\), 因此Newton-CG方法为二阶方法.
关于算法的更多细节可见Numerical Optimization一书算法7.1. 另外通过观察算法不难发现, 若能提供Hseeian-vector products函数, 那么Newton-CG方法此时就是一阶半方法.
Newton-CG方法的主要计算量在CG迭代部分, preconditioning可加速CG迭代过程, 见Numerical Optimization一书page118.
Dogleg法
狗腿法是一种信赖域方法, 简单介绍信赖域方法, 与线搜索方法先确定方向后确定步长不同的是, 信赖域方法在确定方向前首先给定一个信赖域半径\(\Delta\), 要求搜索方向在该信赖域内.
涉及信赖域方法就不得不谈信赖域子问题: \[\min_{p}m_k(p)=f_k+\nabla f_k^Tp_k+\frac{1}{2}p^TB_kp\ \ \operatorname{ s.t. }\Vert p\Vert\le\Delta\]且一般的, 这里的\(B_k\)仅仅要求对称, 一致有界. 关于这点可见Numerical Optimization一书page68; 但具体到这里的狗腿法仍然需要加上正定性的要求.
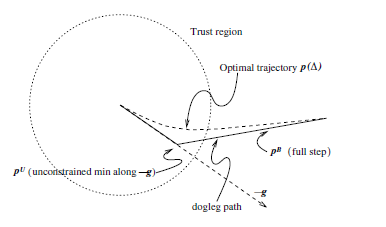
回过头来看狗腿法, 狗腿法实际上是对信赖域子问题最优解曲线的近似, 从图中可以看到, 第一段是沿着负梯度方向到达柯西点, 这里的柯西点指的是沿着负梯度方向极小化信赖域子问题得到的极小值点; 接着像狗腿那样拐弯, 直奔信赖域子问题的最优解而去, 因此信赖域半径的作用就是决定了上述过程能跑多远.
Trust-ncg方法
信赖域Newton-CG方法与Newton-CG方法的区别在于不是直接用CG方法解牛顿方程(\(\nabla^2f_k p_k+\nabla f_k=0\)), 而是解信赖域子问题 \[\min_{p}m_k(p)=f_k+\nabla f_k^Tp_k+\frac{1}{2}p^TB_kp\ \ \operatorname{ s.t. }\Vert p\Vert\le\Delta\] 这里\(B_k=\nabla^2 f_k\). 另外步长可直接设为1而不需要做一维巡查.
与Newton-CG方法类似, 显然Trust-ncg法本身是二阶方法, 但若能提供Hseeian-vector products函数, Trust-ncg方法也是一阶半方法. 算法细节可见Numerical Optimization一书算法7.2.
preconditioning可加速CG迭代过程, 见Numerical Optimization一书page118.
Trust-krylov方法
其实应该叫Trust-Lanczos方法, Lanczos方法可以用来三对角化矩阵, 同时构造出了一个Krylov子空间. 上述过程的应用之一就是用来解线性方程\(Ax=b\), 因此也可解牛顿方程, 参见矩阵计算第三版9.3节.
与Trust-ncg方法相比, Trust-krylov方法只是将CG方法换成了Lanczos方法, 且本身仍为二阶方法, 同样若能提供Hseeian-vector products函数, Trust-krylov方法也是一阶半方法.
Trust-exact方法
exact指的是信赖域子问题 \[\min_{p}m_k(p)=f_k+\nabla f_k^Tp_k+\frac{1}{2}p^TB_kp\ \ \operatorname{ s.t. }\Vert p\Vert\le\Delta\]中的\(B_k=\nabla^2 f_k\)再进行直接求解. 形式上与Trust-ncg方法、Trust-krylov方法非常类似, 但计算量显然要大一些, 因此只适合小规模问题.
显然Trust-exact方法为二阶方法.
有界约束优化
L-BFGS-B方法
To be continued...