前言: 本文主要是关于拉普拉斯近似方法, 这是一种用来近似计算积分的方法, 主要参考了维基百科及PRML一书6.4节.
拉普拉斯近似方法
拉普拉斯近似方法(Laplace's method)是一种近似计算积分的方法, 目标积分形如\[\int_a^be^{Mf(x)}dx\]其中\(f(x)\)要求是二次可微的, \(M\)要求是一个较大的数. 其想法是假定\(x_0\)是\(f(x)\)唯一的最大值点, 因此\(f(x_0)>f(x)\), 乘上一个较大的M, 在经过指数函数的作用, 其差值事实上会变得很大, 不难想象随着\(M\)的增大积分内的函数会越来越像一个单峰函数, 事实上确实会逼近对一个正态分布进行积分的值. 举个例子\(f(x)=sinx/x\), 分别画出\(e^{sinx/x}\)和\(e^{3sinx/x}\)的函数图像: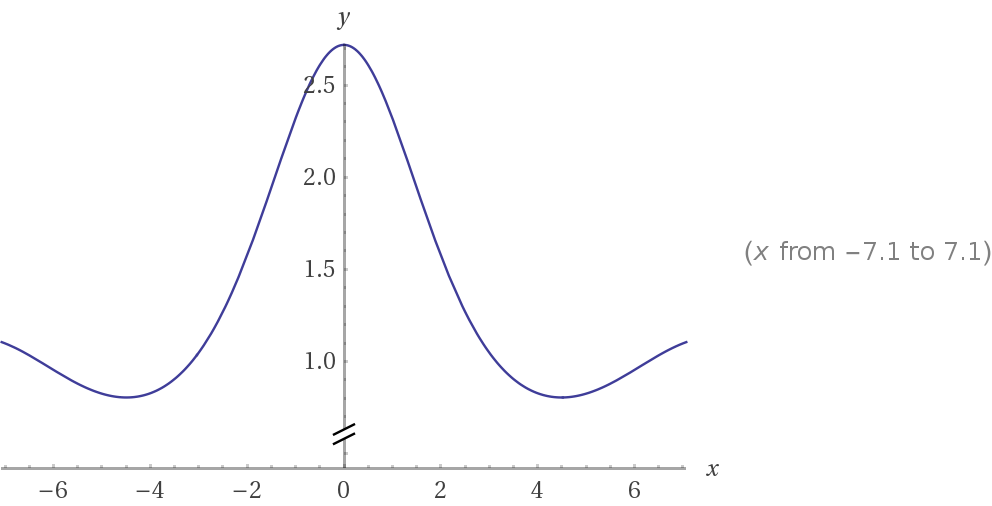
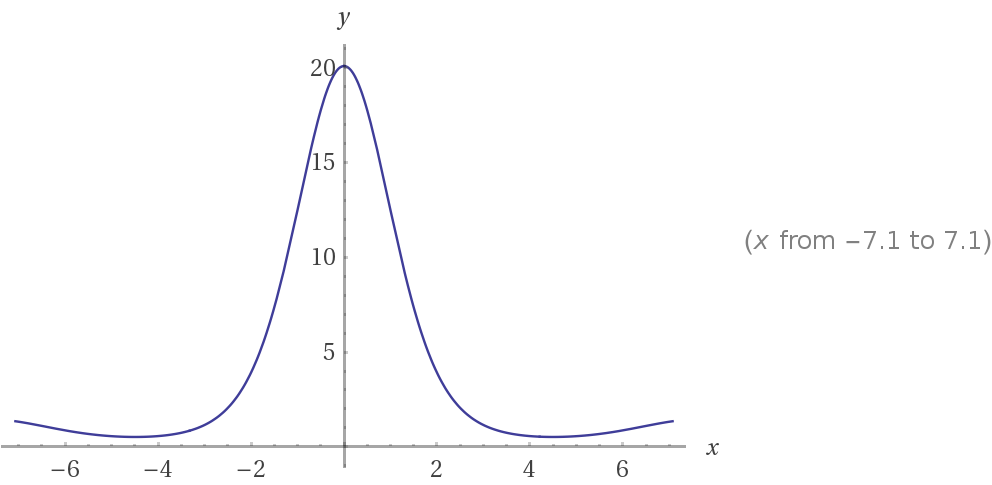
考虑多元情形, 假定\(x_0\)为f(x)的最大值点, 因此有\(\nabla f(x_0)=0\)且Hessian矩阵\(H(x_0)负定\). 将\(f(x)\)在\(x_0\)处泰勒展开得\[f(x)\approx f(x_0)+\frac{1}{2!}(x-x_0)^TH(x_0)(x-x_0)\]此时积分近似为\[\int_a^be^{Mf(x)}dx\approx e^{Mf(x_0)}\int_a^b e^{\frac{M}{2}(x-x_0)^TH(x_0)(x-x_0)}dx\]假设\(x_0\)包含在区间\([a,b]\)内, 那么右式可以直接视为在\((-\infty,+\infty)\)上的积分, 因为随着\(M\)的增大区间之外的积分会越来越小. 而此时右边的积分即为一个对多元正态分布的积分, 且该积分可以通过变量代换\(t=H(x_0)^{\frac{1}{2}}(x-x_0)\)化成标准的多元正态分布计算出来:\[\int_a^b e^{\frac{M}{2}(x-x_0)^TH(x_0)(x-x_0)}dx\approx \int_{-\infty}^{+\infty} e^{\frac{M}{2}(x-x_0)^TH(x_0)(x-x_0)}dx=\left(\frac{2\pi}{M}\right)^\frac{d}{2}\left|-H(x_0)\right|^{-\frac{1}{2}}(M\to+\infty)\]这里的\(d\)指的是自变量\(x\)的维度, \(H(x_0)\)指\(f(x)\)在\(x_0\)处的Hessian矩阵. 因此得到结论:\[\int_a^be^{Mf(x)}dx\approx e^{Mf(x_0)}\left(\frac{2\pi}{M}\right)^\frac{d}{2}\left|-H(x_0)\right|^{-\frac{1}{2}}(M\to+\infty)\]本质上来说, 倘若暂时先不考虑\(M\)的大小, 用二阶泰勒展开对\(f(x)\)进行近似的方法实际上是把被积函数视为多元正态分布. 一元情形的相关定理描述及证明请移步维基百科, 最后来看一个更一般的结论:\[\int_a^bh(x)e^{Mf(x)}dx\approx h(x_0)e^{Mf(x_0)}\left(\frac{2\pi}{M}\right)^\frac{d}{2}\left|-H(x_0)\right|^{-\frac{1}{2}}(M\to+\infty)\]这里要求\(h(x)>0\).
例子
例子参考了PRML一书6.4节, 来自高斯过程分类中的预测问题, 目标也是求一个积分\[P(a_{N+1}\mid t_N)=\int P(a_{N+1}\mid a_N)P(a_N\mid t_N)da_N\]这里的目标变量\(t\in\{0, 1\}\)为二分变量; 被积函数第一部分\(P(a_{N+1}\mid a_N)\)是个正态分布, 即为高斯过程回归做预测时的核心结论. 本质上来说, 拉普拉斯近似方法把被积函数或者是被积函数的一部分代换成多元正态分布\(N(\mu, \Sigma)\), 这里仅把被积函数的第二部分代换掉. 回想多元正态分布的密度函数, 因此只要计算\(\log P(a_N\mid t_N)\)关于变量\(a_N\)的梯度\(\nabla\)和Hessian矩阵\(\nabla^2\), 此时\(\mu\)即为\(\nabla=0\)的解, \(\Sigma=-\nabla^2\). 接着由两个正态分布积分的一些性质(PRML一书2.115), 可以得到目标积分的近似结果仍为一个正态分布. 然后我们可以用它来做预测\[P(t_{N+1}=1\mid t_N)=\int P(t_{N+1}=1\mid a_{N+1})P(a_{N+1}\mid t_N)da_{N+1}\]具体计算时被积函数的第一部分利用自己本身的性质近似成了正态分布的分布函数(而非密度函数)(PRML一书4.153). p.s.: 高斯过程分类中的参数也可以用拉普拉斯近似方法得到, 这里就不再赘述, 最后建议细细读一读PRML一书6.4节.